Курсовая работа: Единое пересечение кривых в пространстве
F′(x′, y ′) = а′22 у′ 2 , а′22 ≠0, F ′(x′, y ′) =b ′22 у′ 2 , b ′22 ≠0.
Полагая λ = b ′22 : a ′22 , получим F ′(x′, y ′)= F′(x′, y ′) —утверждение теоремы верно и в этом случае.
Наконец, в случае 1° уравнения (8) и (9) принимают вид
F′(x′, y ′) = а′22 у′ 2 + a ′0 =0, a ′0 ≠0,
F ′(x′, y ′) = b ′22 у′ 2 + b ′0 =0 b ′0 ≠0
— множество С есть пара прямых, определенная каждым из уравнений
y ′=±(-( a ′0 : a ′22 )0,5 ) или y ′=±(-( b ′0 : b ′22 )0,5 ).
Для того чтобы эти уравнения были эквивалентны, очевидно, необходимо и достаточно, чтобы было
(a′0 : a′22 )=( b′0 : b′22 ), т.е. b′22 =λa′22 , b′0 =λa′0 приλ =( b′22 : a′22 ).
Теорема доказана во всех случаях .
3 Пучок кривых второго порядка
Пусть M1 , M2 , M3 , M4 , — четыре точки, не лежащие на одной прямой. Задавая по произволу еще одну точку M5 (не коллинеарную никаким трем из точек M1 , M2 , M3 , M4 , получим, по теореме 1, единственную кривую второго порядка, проходящую через точки M1 , M2 , M3 , M4 , и точку M5 .
Поэтому множество всех кривых второго порядка, проходящих через четыре точки M1 , M2 , M3 , M4 , бесконечно. Это множество кривых называется пучком кривых второго порядка, определяемым точками M1 , M2 , M3 , M4 .
Будем обозначать кривую той же буквой F , которой обозначена левая часть F(x, у) ее уравнения (1), так что F и λ F при любом λ ≠0 — это одна и та же кривая. Если
F (х, y) = λ 1 F 1 (x, y) + λ 2 F 2 (x, y) ,
то будем говорить, что кривая F есть линейная комбинация (с коэффициентами λ 1 и λ 2 ) кривых F1 и F2 . Если кривые F1 и F2 принадлежат пучку, определяемому точками M i = (x i , y i ) (i = l, 2, 3, 4) , то уравнения F1 (x, у)=0 и F2 (x, у)=0 удовлетворяются, если в них подставить значения х = xi , у = yi при любых i = l, 2, 3, 4 . Но тогда и уравнение λ 1 F 1 (x, y) + λ 2 F 2 (x, y)=0 будет при х = xi , у = yi удовлетворяться. Другими словами, всякая кривая, являющаяся линейной комбинацией двух (или более) кривых, принадлежащих данному пучку, принадлежит этому пучку. Докажем обратное предложение. Пусть в пучке кривых второго порядка выбраны две определенные кривые F1 и F2 . Тогда всякая кривая F данного пучка есть линейная комбинация этих двух кривых F1 и F2 .
Пусть пучок определен четверкой точек M1 , M2 , M3 , M4 . Возьмем на кривой F какую-нибудь точку M5 , не коллинеарную ни с какими тремя из точек M1 , M2 , M3 , M4 . Кривая F есть единственная кривая второго порядка, проходящая через точки M1 , M2 , M3 , M4 , M5 . Поэтому для доказательства сделанного утверждения достаточно найти такую линейную комбинацию λ 1 F 1 + λ 2 F 2 чтобы кривая
λ 1 F 1 (x, y) + λ 2 F 2 (x, y)=0 (12)
проходила через точку M5 = (х5 , у5 ), т. е. достаточно определить λ 1 и λ 2 , вернее, их отношение λ 1 :λ 2 , из условия
λ 1 F 1 (х5 , у5 ) + λ 2 F 2 (х5 , у5 ) , (13)
Итак, любой пучок кривых второго порядка вполне определен, если даны две какие-нибудь кривые F 1 и F 2 из этого пучка: он состоит из всех кривых, являющихся линейными комбинациями λ 1 F 1 + λ 2 F 2 двух данных. Все эти кривые определяются значениями одного параметра— отношением λ = λ1 : λ 2 двух коэффициентов в линейной комбинации λ 1 F 1 + λ 2 F 2 . Другими словами, пучок кривых второго порядка является одномерным многообразием кривых — совершенно в том же смысле, в каком пучок прямых является одномерным многообразием прямых (а пучок плоскостей —
 |
?????????? ????????????? ??????????).
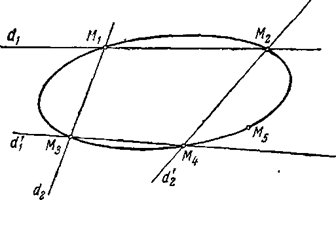
Понятие пучка кривых позволяет очень просто найти уравнение кривой второго порядка, проходящей через заданные пять точек M1 , M2 , M3 , M4 , M5 . В самом деле, возьмем четыре точки из числа данных пяти, например M1 , M2 , M3 , M4 .
Легко написать уравнения прямых:
d 1 : M 1 M 2 d ′1 : M 3 M 4 ,
d 2 : M 1 M 3 d ′2 : M 2 M 4 .
Теперь имеем две распадающиеся кривые второго порядка: кривую F1 распадающуюся на пару прямых d 1 и d ′1 , и кривую F2 , распадающуюся на прямые d 2 и d ′2 . Многочлены F1 (х, у) и F2 (х, у) суть произведения трехчленов первой степени, являющихся левыми частями уравнений, соответствующих прямым d 1 и d ′1 , d 2 и d ′2 . Распадающиеся линии F1 и F2 , очевидно, проходят через точки M1 , M2 , M3 , M4 т. е. принадлежат пучку, определяемому этими точками. Остается только определить отношение λ1 : λ 2 из условия, чтобы кривая λ 1 F 1 + λ 2 F 2 проходила через точку M5 = (х5 , у5 ), этим условием является равенство (13), из которого находим
λ1 : λ 2 = - F 2 (х5 , y 5 ) : F 1 ( x 5 , у5 ).
4 Теорема единственности для поверхностей второго порядка
Теорема 3 . Два многочлена второй степени F1 (x, у, z) и F2 (х, y , z) тогда и только тогда имеют одно и то же нулевое многообразие, когда они пропорциональны между собою, т. е. когда один из них получается из другого умножением на некоторое число λ ≠0 .
Как н в случае многочленов от двух переменных, только одна половина этой теоремы нуждается в доказательстве: надо доказать, что два многочлена второй степени F1 (x, у, z) и F2 (х, y , z) , имеющие одно и то же нулевое многообразие CF 1 = CF 2 = C , пропорциональны между собою.
Рассмотрим поверхности