Курсовая работа: Электрические цепи с нелинейными преобразователями и оперативная коррекция режима энергосистемы

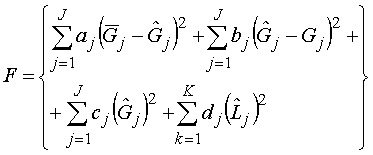(6)

при условиях (1-5), где - известные весовые коэффициенты. В этой функции

ü первый член отражает требование минимизации отклонения узловых мощностей от плановых или прогнозных значений,

ü второй член отражает требование минимизации отклонения узловых мощностей от измеренных значений, т.е. минимизации изменения генерируемых мощностей,

ü третий член отражает требование минимизации стоимости генерации мощности,

ü четвертый член отражает требование минимизации потерь в линиях электропередач.

6. Математическая модель оперативной коррекции

Математическая нелинейная модель оперативной коррекции учитывает, что

узловая мощность равна алгебраической сумме перетоков по линиям, соединенным с данным узлом (1),

перетоки зависят от разности фаз узловых напряжений на концах линии электропередач (2, 3).

Заметим, что можно рассмотреть линейную модель оперативной коррекции [5], где энергосистема представлена уравнением, связывающим узловые мощности и перетоки коэффициентами влияния (узловых мощностей на перетоки). Эти коффициенты сохраняют определенное значение в узком диапазоне режимов. В связи с этим и предлагается данная модель.

Различные варианты математической нелинейной модели рассматривались в [3, 6, 7]. В данном случае математическая нелинейная модель в целом состоит из уравнений (5.1-5.6) Для решения сформулированной выше задачи воспользуемся методом неопределенных множителей Лагранжа, обозначив их через для условий (5.1, 5.2, 5.3) соответственно. При этом задача превратится в задачу минимизации функции

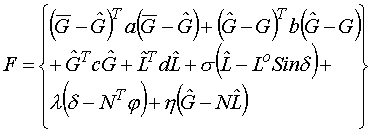(1)

при нелинейных ограничениях (5.4, 5.5), что эквивалентно решению системы уравнений (5.1-5.5) и

(2)

(3)

(4)

(5)

Последние уравнения получены дифференцированием (1) по соответственно. Объединяя (2) и (3), получаем:

(6)

Таким образом, исходная задача сводится к решению системы уравнений (5.1-5.5, 4, 5, 6) относительно неизвестных , где известны .

Важно отметить, что для решения задачи не нужно измерять фазы напряжений. Однако, после решения задачи эти фазы становятся известными.

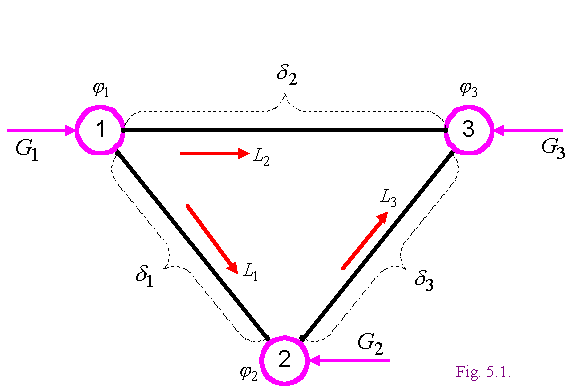
7. Электрическая цепь, как модель оперативной коррекции

Рассмотрим сдвоенную электрическую цепь с синусно-косинусными преобразователями СКП, как модель оперативной коррекции в энергосистеме (ср. также с фиг. 4.1 и см. также [3, 6, 7]). Будем использовать в ней для обозначения токов, потенциалов, напряжений и сопротивлений те же символы, которые использованы для обозначения параметров энергосистемы. Итак,

- первичный ток СКП,

- вторичный ток СКП,

- первичное напряжение СКП,

- вторичное напряжение СКП,

- токи второй (из сдвоенных) цепи,

- потенциалы первой (из сдвоенных) цепи,