Курсовая работа: Электрические цепи с нелинейными преобразователями и оперативная коррекция режима энергосистемы
![]() - токи источников тока второй (из сдвоенных) цепи,
- токи источников тока второй (из сдвоенных) цепи,
![]() - сопротивления второй (из сдвоенных) цепи,
- сопротивления второй (из сдвоенных) цепи,
![]() - сопротивления первой (из сдвоенных) цепи,
- сопротивления первой (из сдвоенных) цепи,
![]() - коэффициент преобразования СКП,
- коэффициент преобразования СКП,
![]() - напряжения в первой (из сдвоенных) цепи.
- напряжения в первой (из сдвоенных) цепи.
Пример 7.1. Моделирующую электрическую цепь удобно рассмотреть для энергосистемы, которая представленна в примере 5.1 - см. фиг. 7.1, где
MF - модель ограничителя разности фаз,
ML - модель линии электропередач,
MG - модель узла (генерирующего или нагрузочного),
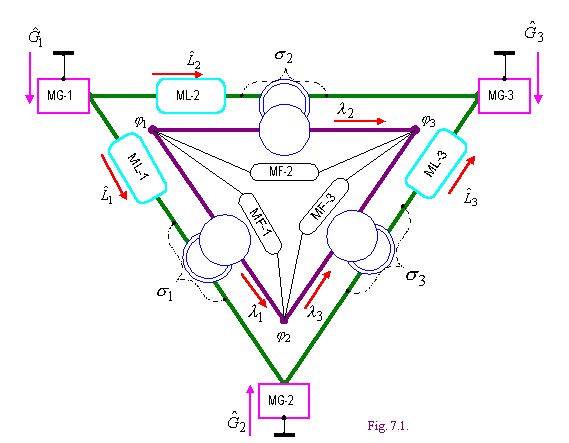
Рассмотрим отдельные блоки моделирующей электрической цепи.
Модель СКП с коэффициентом преобразования ![]() рассмотрена в примере 1.
рассмотрена в примере 1.
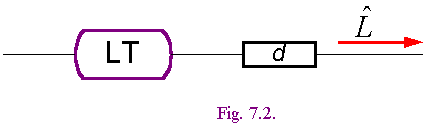
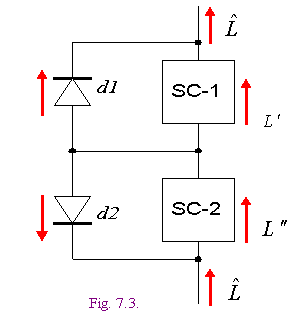
Модель ML линии электропередач представлена на фиг. 7.2, где ![]() - сопротивление, LT - ограничитель тока. Конструкция ограничителя представлена на фиг. 7.3, где SC1, SC2 -источники тока, d1, d2 - диоды. Этот ограничитель реализует неравенство (5.5).
- сопротивление, LT - ограничитель тока. Конструкция ограничителя представлена на фиг. 7.3, где SC1, SC2 -источники тока, d1, d2 - диоды. Этот ограничитель реализует неравенство (5.5).
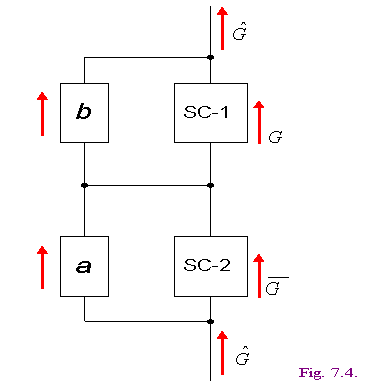
Модель MG узла энергосистемы представлена на фиг. 7.4, где
ток источника тока SC-1 иммитирует генерируемую в узле мощность, измеренную в данный момент;
ток ![]() источника тока SC-2 иммитирует плановое значение генерируемой в узле мощности или прогноз нагрузки;
источника тока SC-2 иммитирует плановое значение генерируемой в узле мощности или прогноз нагрузки;
ток в сопротивлении b иммитирует отклонение генерируемой мощности от текущего значения (как показано выше, оно минимизируется);
ток ![]() в сопротивлении a иммитирует задание на изменение генерируемой мощности (как показано выше, оно минимизируется); для нагрузочного узла a=0;
в сопротивлении a иммитирует задание на изменение генерируемой мощности (как показано выше, оно минимизируется); для нагрузочного узла a=0;
ток , протекающий через MG , иммитирует измененное значение узловой мощности.
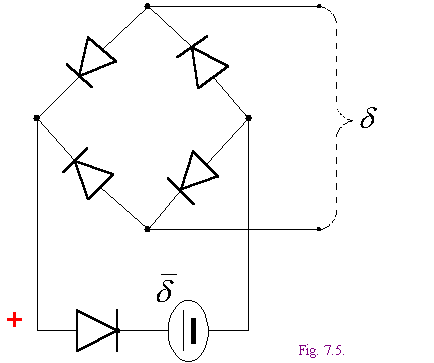
Модель MF ограничителя разности фаз изображена на фиг. 7.5. Она представляет собой мостовую схему, преобразующую напряжение ![]() в напряжение заданного направления
в напряжение заданного направления![]() . Из схемы ясно, что напряжение
. Из схемы ясно, что напряжение ![]() не может превышать напряжение источника
не может превышать напряжение источника![]() . Тем самым моделируется неравенство (5.4).
. Тем самым моделируется неравенство (5.4).
Таким образом, рассматриваемая электрическая цепь моделирует задачу оперативной коррекции. В этой цепи минимизируется функция (6.1) при нелинейных ограничениях (5.4, 5.5), а выполнение условия (5.4) обеспечивает существование глобального минимума этой функции.
8. О методе расчета
В программе расчитывается описанная выше электрическая цепь постоянного тока с нелинейными элементами. Назовем эту цепь базовой. Базовая электрическая цепь модифицируется таким образом, что она становится моделью задачи выпуклого программирования без ограничений - безусловного выпуклого программирования. Назовем такую цепь безусловной. Выбор величины некоторого параметра безусловной электрической цепи (названного методическим сопротивлением) позволяет сделать расчетные параметры (токи в ветвях и потенциалы) базовой и безусловной электрических цепей сколь угодно близкими. С другой стороны, расчет безусловной электрической цепи сводится к поиску единственного минимума без ограничений. Для решения такой задачи существует быстродействующий метод градиентного спуска.
В программе использован метод сопряженного градиента [8]. При этом существует обратная зависимость между точностью и временем решения. На практике это означает, что диспетчер может быстро перебирать приближенные варианты оптимизации (варьируя уставки), а затем более точно расчитать выбранный вариант.
Список литературы
1. Деннис Дж. Б. Математическое программирование и электрические цепи. М.: ИЛ, 1961, 430 с. Dennis Jack B. Mathematical Programming and Electrical Networks, New York, 1959, Pages V1, 186 p.
2. Хмельник С. И. Электрические цепи для моделирования задач квадратичного программирования, ж. "Электронное моделирование", 1990, том 12, N4.