Курсовая работа: Еліптичні інтеграли

і .

5) А = -1, (h>h’>0). Змінна t може змінюватися лише між і . Припустимо

, де 0<z<1.

Маємо

і Цим вичерпуються всі можливі випадки, тому що у випадку, коли А = -1 і обидва числа m, m’ > 0, радикал взагалі не міг би мати дійсних значень. Про множник ми не говорили нічого, тому що у всіх випадках він, очевидно, перетворювався у раціональну функцію від .

Відмітимо ще, що розглядаючи інтеграл (8), ми можемо обмежуватися значеннями z<1; випадок приводиться до цього підстановкою , де <1.

4. Еліптичні інтеграли 1-го, 2-го і 3-го роду

Тепер залишається вивчити найпростіші з інтегралів виду (8), до яких можна було б звести всі інтеграли цього виду, а відповідно, в кінцевому рахунку, і взагалі, всі еліптичні інтеграли.

Виділимо з раціональної функції R(x), що зустрічається в підінтегральному виразі (8) цілу частину P(x), а правильний дріб, який входить до його складу, розкладемо на прості дроби. Якщо не об’єднувати спряжені комплексні корені знаменника, а розглядати їх окремо, як дійсні корені, то R(x) представиться у вигляді суми степенів (n = 0, 1, 2,…) і дробів виду (m = 1, 2, 3,…), де а може бути і уявним числом, помножених на числові коефіцієнти. Звідси ясно, що інтеграл (8), в загальному випадку, являється лінійним агрегатом наступних інтегралів:

(n = 0, 1, 2,…)

і (m = 1, 2, 3,…).

Зупинимося на інтегралах . Якщо проінтегрувати тотожність

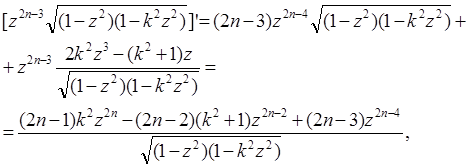
то отримаємо рекурентне співвідношення

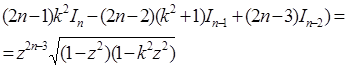(9)

що зв’язують три послідовні інтеграли І. Припускаючи що тут n=2, виразимо через та ; якщо взяти n=3 і замість підставити його вираз через та , то навіть виразиться через ці інтеграли. Продовжуючи так далі, легко переконатися, що кожен з інтегралів виражається через та і далі враховуючи (9), можна встановити і вигляд з’єднуючої їх формули

де і - постійні, а є непарний многочлен степені (2n-3). Звідси стає зрозумілим, що якщо є многочлен n – ї степені від х, то

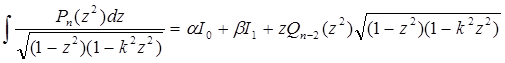, (10)

де і - постійні, а (х) є деякий многочлен (n-2) – ї степені від х. Визначення цих постійних і коефіцієнтів многочлена Q може бути виконано (якщо многочлен Р коректно заданий за методом невизначених коефіцієнтів.)

Зауважимо, що з (9) можна було б виразити через та інтеграли і при від’ємних значеннях (n= -1, -2, …), так що в інтегралах досить обмежитись випадком .

Переходячи до інтегралів (скажімо, при дійсних a), подібним чином встановимо для них рекурентне співвідношення

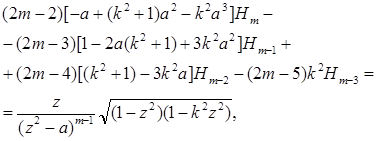
справедливе і при від’ємних і нульовому значеннях m.

Звідси всі виражаються через три з них:

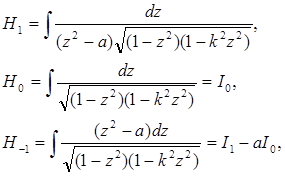
тобто, кінцево через , та .

Підкреслимо, що усе це зберігає силу і при уявних значеннях параметра а.