Курсовая работа: Еліптичні інтеграли
|
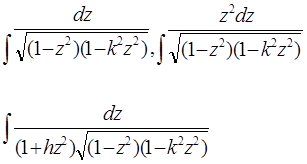
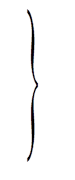
( останній інтеграл виходить із 
введенням, замість 
, нового параметра 
). Ці інтеграли, як показав Ліувіль , в кінцевому виді вже не беруться. Лежандр їх назвав еліптичними інтегралами, відповідно, 1-го, 2-го і 3-го роду. Перші два містять лише один параметр k, а останній, крім нього, ще (комплексний) параметр h.
Лежандр вніс у ці інтеграли ще подальші спрощення, виконавши в них підстановку 
(
змінюється від 0 до 
). При цьому перший із них безпосередньо переходить в інтеграл
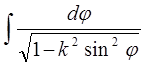. (11)
Другий перетворюється так:
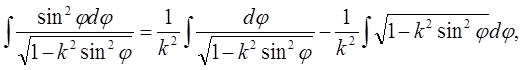
тобто приводиться до попереднього інтеграла і до нового інтеграла
. (12)
Нарешті, третій інтеграл при вказаній підстановці переходить в
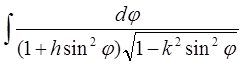. (13)
Інтеграли (11), (12) і (13) також називаються еліптичними інтегралами 1-го, 2-го і 3-го роду – в формі Лежандра.
Із них особливо важливе значення і застосування мають перші два. Якщо враховувати, що ці інтеграли при 
перетворюються в нуль, і тим зафіксувати вільні сталі, що містяться в них, то отримаємо дві доволі визначені функції від 
, які Лежандр позначив відповідно через F(k, φ) і E(k, φ). Тут, крім незалежної змінної , вказаний також параметр k, що називається модулем, який входить у вирази цих функцій.
Лежандром були складені обширні таблиці значень цих функцій при різних і різних k. В них не тільки аргумент ,який трактуються як кут, що виражається в градусах, але і модуль kрозглядається як синус деякого кута
, який і вказується в таблиці замість модуля, причому також в градусах.
Крім того, як Лежандром, так і іншими вченими були вивчені найглибші властивості цих функцій, встановлений ряд формул, що відносяться до них, і т.д.
Дякуючи цьому функції F і E Лежандра ввійшли в сім’ю функцій, що зустрічаються в аналізі і його додатках, на рівних правах з елементарними функціями.
Висновки
В результаті усіх наших міркувань ми коротко можемо сказати, що всі еліптичні інтеграли за допомогою елементарних підстановок – з точністю до доданків, що виражаються в кінцевому виді, - приводяться до наступних трьох стандартних інтегралів Лежандра:
|
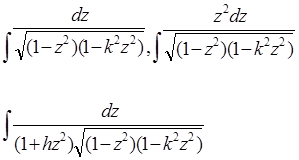
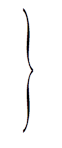
А за допомогою підстановки 
(
змінюється від 0 до 
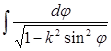) ці інтеграли перетворюються в такі:
, і ,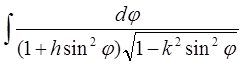
які також називаються еліптичними інтегралами 1-го, 2-го і 3-го роду в формі Лежандра, значення яких можна знайти в таблицях.
Використана література:
1. Г.М. Фихтенгольц. Курс дифференциального и интегрального исчисления. Том I. М.: Наука, 1966 г., 800 стр. с илл.
2. Г.М. Фихтенгольц. Курс дифференциального и интегрального исчисления. Том II. М.: Наука, 1966 г., 800 стр. с илл.
3. Г. Корн, Т. Корн. Справочник по математике для научных работников и инженеров. М.: Наука, 1973 г., 832 стр. с илл.
4. И.Н. Бронштейн, К.А. Семендяев. Справочник по математике для инженеров и учащихся вузов. М.: Наука, 1980 г., 976 с., илл.
ДОДАТКИ
Еліптичні інтеграли першого роду
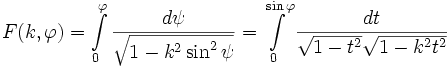
Еліптичні інтеграли першого роду | ||||||||||
| 0° | 10° | 20° | 30° | 40° | 50° | 60° | 70° | 80° | 90° | |
| 0° | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 10 | 0.1745 | 0.1746 | 0.1746 | 0.1748 | 0.1749 | 0.1751 | 0.1752 | 0.1753 | 0.1754 | 0.1754 |
| 20 | 0.3491 | 0.3493 | 0.3499 | 0.3508 | 0.3520 | 0.3533 | 0.3545 | 0.3555 | 0.3561 | 0.3564 |
| 30 | 0.5236 | 0.5243 | 0.5263 | 0.5294 | 0.5334 | 0.5379 | 0.5422 | 0.5459 | 0.5484 | 0.5493 |
| 40 | 0.6981 | 0.6997 | 0.7043 | 0.7116 | 0.7213 | 0.7323 | 0.7436 | 0.7535 | 0.7604 | 0.7629 |
| 50 | 0.8727 | 0.8756 | 0.8842 | 0.8982 | 0.9173 | 0.9401 | 0.9647 | 0.9876 | 1.0044 | 1.0107 |
| 60 | 1.0472 | 1.0519 | 1.0660 | 1.0896 | 1.1226 | 1.1643 | 1.2126 | 1.2619 | 1.3014 | 1.3170 |
| 70 | 1.2217 | 1.2286 | 1.2495 | 1.2853 | 1.3372 | 1.4068 | 1.4944 | 1.5959 | 1.6918 | 1.7354 |
| 80 | 1.3963 | 1.4056 | 1.4344 | 1.4846 | 1.5597 | 1.6660 | 1.8125 | 2.0119 | 2.2653 | 2.4362 |
| 90 | 1.5708 | 1.5828 | 1.6200 | 1.6858 | 1.7868 | 1.9356 | 2.1565 | 2.5046 | 3.1534 |  |