Курсовая работа: Гипергеометрическое уравнение
Сумма ряда
F(![]() ,
, ![]() ,
, ![]() ,z) =
,z) = ![]() ,
, ![]() <1 (1.1)
<1 (1.1)
называется гипергеометрической функцией.
Данное определение гипергеометрической функции пригодно лишь для значений z, принадлежащих кругу сходимости, однако в дальнейшем будет показано, что существует функция комплексного переменного z, регулярная в плоскости с разрезом (1, ![]() ) которая при
) которая при ![]() <1 совпадает с F(
<1 совпадает с F(![]() ,
, ![]() ,
, ![]() ,z). Эта функция является аналитическим продолжением F(
,z). Эта функция является аналитическим продолжением F(![]() ,
, ![]() ,
, ![]() ,z) в разрезанную плоскость и обозначается тем же символом.
,z) в разрезанную плоскость и обозначается тем же символом.
Чтобы выполнить аналитическое продолжение предположим сначала что R(![]() )>R(
)>R(![]() )>0 и воспользуемся интегральным представлением
)>0 и воспользуемся интегральным представлением
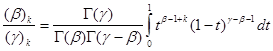 (1.2)
(1.2)
k=0,1,2,..
Подставляя (1.2) в (1.1) находим
F(![]() ,
, ![]() ,
, ![]() ,z) =
,z) = 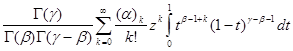 = =
= =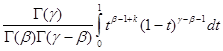
![]() ,
,
причем законность изменения порядка интегрирования и суммирования вытекает из абсолютной сходимости.
Действительно, при R(![]() )>R(
)>R(![]() ) >0 и
) >0 и ![]() <1
<1
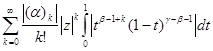
![]()
![]()
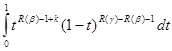
![]() =
=
=![]() F(
F(![]() , R(
, R(![]() ),R(
),R(![]() ),
),![]() )
)
На основании известного биноминального разложения
![]() =(1-tz)- a (1.3)
=(1-tz)- a (1.3)
0![]() t
t![]() 1,
1,![]() <1
<1
поэтому для F(![]() ,
, ![]() ,
, ![]() ,z) получается представление
,z) получается представление
F(![]() ,
, ![]() ,
, ![]() ,z)=
,z)=  (1.4)
(1.4)
R(![]() )>R(
)>R(![]() ) >0 и
) >0 и ![]() <1
<1
Покажем, что интеграл в правой части последнего равенства сохраняет смысл и представляет регулярную функцию комплексного переменного zв плоскости с разрезом (1, ![]() ).
).
Для zпринадлежащих области ![]() ,
, ![]() (R– произвольно большое,
(R– произвольно большое, ![]() и
и ![]() произвольно малые положительные числа), и 0 < t< 1 подынтегральное выражение есть регулярная функция zи непрерывная функция t ; поэтомудостаточно показать что интеграл сходится равномерно в рассматриваемой области. Доказательство следует из оценки
произвольно малые положительные числа), и 0 < t< 1 подынтегральное выражение есть регулярная функция zи непрерывная функция t ; поэтомудостаточно показать что интеграл сходится равномерно в рассматриваемой области. Доказательство следует из оценки
![]()
(М – верхняя граница модуля функции (1-tz)- a , непрерывной в замкнутой области ![]() ,
, ![]() , 0
, 0![]() t
t![]() 1), которая показывает, сходимость интеграла будет мажорированной, то есть при R(
1), которая показывает, сходимость интеграла будет мажорированной, то есть при R(![]() )>R(
)>R(![]() ) >0 интеграл
) >0 интеграл 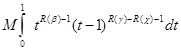 сходится.
сходится.
Таким образом, условие ![]() <1 в (1.4) может быть отброшено, и искомое аналитическое продолжение гипергеометрической функции в разрезанную плоскость дается формулой
<1 в (1.4) может быть отброшено, и искомое аналитическое продолжение гипергеометрической функции в разрезанную плоскость дается формулой
F(![]() ,
, ![]() ,
, ![]() ,z)=
,z)=  (1.5)
(1.5)
R(![]() )>R(
)>R(![]() ) >0;
) >0; ![]()
В общем случае, когда параметры имеют произвольные значения, аналитическое продолжение F(![]() ,
, ![]() ,
, ![]() ,z) плоскость с размером (1,
,z) плоскость с размером (1, ![]() ) может быть получено в форме контурного интеграла, к которому приводит суммирование ряда (1.1) с помощью теории вычетов.
) может быть получено в форме контурного интеграла, к которому приводит суммирование ряда (1.1) с помощью теории вычетов.
Более элементарный метод продолжения, не дающий, однако, возможность получить в явной форме общее аналитическое выражение гипергеометрической функции, заключается в использовании рекуррентного соотношения (1.6)
![]() F(
F(![]() ,
, ![]() ,
, ![]() ,z)=
,z)=![]() +
+![]()