Курсовая работа: Интегрирование и дифференцирование интегралов, зависящих от параметра
3) при каждом фиксированном ![]() функция
функция ![]() регулярна по
регулярна по ![]() в области
в области ![]() .
.
Тогда интеграл (1) есть регулярная в области ![]() функция.
функция.
Доказательство. В силу условий 1, 2 функция ![]() непрерывна в области
непрерывна в области ![]() . Возьмем произвольную точку
. Возьмем произвольную точку ![]() и построим круг
и построим круг ![]() , который содержит точку
, который содержит точку ![]() и лежит внутри
и лежит внутри ![]() . Применим теорему Морера. Пусть
. Применим теорему Морера. Пусть ![]() - замкнутая кривая, лежащая в круге
- замкнутая кривая, лежащая в круге ![]() . Тогда
. Тогда
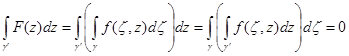 ,(2)
,(2)
так как порядок интегрирования можно переставить, а интеграл по ![]() равен нулю (интегральная теорема Коши). По теореме Морера функция
равен нулю (интегральная теорема Коши). По теореме Морера функция ![]() регулярна в круге
регулярна в круге ![]() ; следовательно,
; следовательно, ![]() регулярна в области
регулярна в области ![]() .
.
Следствие 1. Пусть ![]() - неограниченная кусочно-гладкая кривая, пусть выполнены условия 2, 3 и следующее условие:
- неограниченная кусочно-гладкая кривая, пусть выполнены условия 2, 3 и следующее условие:
4) интеграл (1) сходится равномерно по ![]() , где
, где ![]() - любая замкнутая подобласть области
- любая замкнутая подобласть области ![]() .
.
Тогда функция ![]() регулярна в области
регулярна в области ![]() .
.
Следствие 2. Пусть условия 1, 3 выполнены, но функция ![]() может имеет особенности в концах кривой
может имеет особенности в концах кривой ![]() . Если функция
. Если функция ![]() непрерывна по
непрерывна по ![]() при
при ![]() ,
, ![]() не принадлежит концам
не принадлежит концам ![]() и выполнено условие 4, то функция
и выполнено условие 4, то функция ![]() регулярна в области
регулярна в области ![]() .
.
Доказательство следствий 1 и 2 проводится точно также, как и в теореме 1; интегралы в (2) можно переставлять в силу равномерной сходимости интеграла (1).
Теорема 2. [7, c.112] Пусть выполнены условия теоремы 1. Тогда
![]() .(3)
.(3)
Доказательство . Пусть ![]() - круг
- круг ![]() , лежащий в области
, лежащий в области ![]() и
и ![]() - его граница. Тогда при
- его граница. Тогда при ![]() имеем
имеем

Перестановка порядка интегрирования возможна в силу непрерывности подынтегральной функции и конечности кривых ![]() .
.
Замечание. Теорема 2 остается в силе, если выполнены условия следствия 1 или 2, и интеграл (3) сходится равномерно по ![]() , где
, где ![]() - любая замкнутая подобласть области
- любая замкнутая подобласть области ![]() .
.
Аналитические свойства интегральных преобразований.
Наиболее употребляемыми в математической физике интегральными преобразованиями являются преобразования Лапласа, Фурье и Меллинга.
Пусть функция ![]() определена на полуоси
определена на полуоси ![]() . Ее преобразованием Лапласа называется функция
. Ее преобразованием Лапласа называется функция
 .(4)
.(4)
Теорема 3. [7, c.113] Пусть функция ![]() непрерывна при
непрерывна при ![]() и удовлетворяет оценке
и удовлетворяет оценке
![]() (5)
(5)
Тогда ее преобразование Лапласа ![]() есть функция, регулярная в полуплоскости
есть функция, регулярная в полуплоскости ![]() .
.
Доказательство. Воспользуемся следствием 1 из теоремы 1. Условия 2, 3 теоремы 1 выполнены. Пусть ![]() . Тогда
. Тогда
![]() .
.
Так как  сходится, то по признаку Вейерштрасса интеграл (4) сходится равномерно по
сходится, то по признаку Вейерштрасса интеграл (4) сходится равномерно по ![]() при
при ![]() и функция
и функция ![]() регулярна в этой полуплоскости. В силу произвольности
регулярна в этой полуплоскости. В силу произвольности ![]() функция
функция ![]() регулярна при
регулярна при ![]() .
.
Преобразованием Фурье функции ![]() определенной на действительной оси, называется функция
определенной на действительной оси, называется функция
![]() (6)
(6)
Теорема 4. [7, c.113] Пусть функция ![]() непрерывна при
непрерывна при ![]() и удовлетворяет оценкам
и удовлетворяет оценкам
![]() , (7)
, (7)