Курсовая работа: Интегрирование и дифференцирование интегралов, зависящих от параметра

Для доказательства этой теоремы достаточно повторить предыдущие рассуждения соответствующее число раз. Итак, если функция является аналитической функцией в области , то в этой области функция обладает непрерывными производными всех порядков. Это свойство аналитической функции комплексной переменной существенным образом отличает ее от функции действительной переменной, имеющей непрерывную первую производную в некоторой области. В последнем случае из существования первой производной, вообще говоря, не следует существование высших производных.

Рассмотрим ряд важных следствий установленного свойства аналитической функции комплексной переменной.

Теорема 8(Морера). [6, c.59]Пусть функция является непрерывной в односвязной области и интеграл от по любому замкнутому контуру, целиком принадлежащему , равен нулю. Тогда является аналитической функцией в области .

Доказательство. Было доказано, что при условиях теоремы функция

,

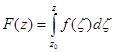где , - произвольные точки области , а интеграл берется по любому пути, соединяющему эти точки в области , является аналитической в этой области функцией, причем . Но, как только что было установлено, производная аналитической функции также является аналитической функцией, т. е. существует непрерывная производная функции , а именно функция , что и доказывает теорему.

Отметим, что теорема 1.10 является в определенном смысле обратной по отношению к теореме Коши. Ее легко обобщить и на многосвязные области.

Теорема 9(Лиувилля). [6, c.59] Пусть на всей комплексной плоскости функция является аналитической, а ее модуль равномерно ограничен. Тогда эта функция тождественно равна постоянной.

Доказательство. Запишем значение производной в произвольной точке по формуле (18):

,

причем будем вести по окружности некоторого радиуса с центром в точке . т.е. . По условию теоремы существует такая константа , что независимо от . Поэтому

.

Так как радиус можно выбрать сколь угодно большим, а не зависит от , то . В силу произвольности выбора точки заключаем, что на всей комплексной плоскости. Отсюда следует, что .

3.3 Вывод формулы Коши

Пусть функция является аналитической в односвязной области , ограниченной контуром . Возьмем произвольную внутреннюю точку и построим замкнутый контур , целиком лежащий в и содержащий точку внутри себя. Рассмотрим вспомогательную функцию

(21)

Функция , очевидно, является аналитической функцией всюду в области , за исключением точки . Поэтому, если мы в области возьмем такой замкнутый контур , лежащий внутри , чтобы точка попала внутрь области, ограниченной контуром , то функция будет аналитической в двухсвязной области , заключенной между контурами и . Согласно теореме Коши интеграл от функции по кривой равен нулю:

Изменив направление интегрирования во втором интеграле, это равенство можно переписать в виде

(22)

Поскольку интеграл, стоящий слева, не зависит от выбора контура то этим свойством обладает и интеграл, стоящий справа. Для дальнейших рассмотрений удобно в качестве контура интегрирования выбрать окружность некоторого радиуса с центром в точке (Рис. 1). Положив ,имеем.

Последний интеграл преобразуем следующим образом:

(23)

Устремим теперь к нулю. Так как - аналитическая, а следовательно, непрерывная функция в области , то для любого положительного числа можно указать такое значение , что для . Отсюда следует, что при существует предел

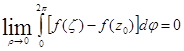
Так как в формуле (23) последнее слагаемое не зависит от то

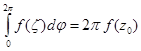, а следовательно и согласно (22)

(24)

Интеграл, стоящий в правой части, выражает значение аналитической функции в некоторой точке через ее значения на любом контуре , лежащем в области аналитичности функции и содержащем точку внутри. Этот интеграл и называется интегралом Коши. Формула (24) часто называется формулой Коши.