Курсовая работа: Интегрирование и дифференцирование интегралов, зависящих от параметра

.

Так как - конечная кривая, то знаменатель при достаточно малых и функция регулярна в точке в силу теоремы 1.

2. Пусть - бесконечная кривая. Ограничимся, для простоты случаем, когда - вещественная ось; тогда

(12)

Пусть функция удовлетворяет оценке

(13)

Покажем, что тогда формула (12) определяет две функции , которые регулярны в полуплоскостях , соответственно. Воспользуемся следствием 1.Рассмотрим случай . Пусть лежит в полуполосе : , где , . При вещественных и при имеем , если . Следовательно,

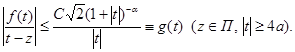
Поскольку интеграл сходится, то по признаку Вейерштрасса интеграл сходится равномерно по . В силу следствия 1 функция регулярна при ; так как можно выбрать сколь угодно большим, а - сколь угодно малым, то интеграл (12) представляет функцию , регулярную в верхней полуплоскости. Аналогично доказывается, что интеграл (12) представляет функцию , регулярную в нижней полуплоскости.

Пример 1. [7, c.119] Пусть функция непрерывна на полуоси и удовлетворяет оценке . Тогда интеграл типа Коши представляет функцию, регулярную в плоскости с разрезом по полуоси .

3. Если функция регулярная на контуре интегрирования , то интеграл типа Коши допускает аналитическое продолжение через точки контура. Прием, который при этом используется, заключается в том, что мы сдвигаем контур интегрирования.

Пример 2. [7, c.119] Пусть

.

Функция регулярна в круге . Покажем, что функцию можно аналитически продолжить на всю комплексную плоскость . Положим при

.

Функция регулярна в круге . Покажем, что

.

тем самым наше утверждение будет доказано. Подынтегральная функция регулярна в кольце , если , так как функция регулярна при всех .

Следовательно, в силу интегральной теоремы Коши интегралы по окружностям и от функции равны при что и требовалось доказать.

Этот пример допускает следующее обобщение. Рассмотрим интеграл типа коши (11), где - простая замкнутая кривая. Тогда этот интеграл определяет функцию, регулярную в области , лежащей внутри .

Пусть функция регулярна в замкнутой области , ограниченной кривыми и , где - простая замкнутая кривая, и лежит внутри . Тогда формула

дает аналитическое продолжение функции в область , лежащую внутри . Действительно, функция регулярна в области , если , так что в силу интегральной теоремы Коши

.

Интеграл в левой части этой формулы задает функцию, регулярную в , а интеграл в правой части равен . Следовательно, , и наше утверждение доказано.

Аналогичный метод применим к интегралам вида (12).

Теорема 6. [7, c.120] Пусть функция регулярна в полосе и удовлетворяет условию

.

Тогда интеграл (2) допускает аналитическое продолжение в полуплоскость и это продолжение дается формулой