Курсовая работа: Інтерполювання функцій
 .
.
Тоді по заданим ![]() однозначно визначаються коефіцієнти
однозначно визначаються коефіцієнти ![]() . В якості системи лінійно незалежних функцій
. В якості системи лінійно незалежних функцій ![]() частіше обирають: степеневі функції
частіше обирають: степеневі функції ![]() (в цьому випадку
(в цьому випадку ![]() - поліном степені п); тригонометричні функції
- поліном степені п); тригонометричні функції ![]() (f - тригонометричний поліном); використовують також раціональні функції та ін.
(f - тригонометричний поліном); використовують також раціональні функції та ін.
В даній курсовій роботі розглядаються інтерполяційні поліноми.
Відомо, що будь-яка неперервна на відрізку ![]() функція
функція ![]() може бути добре наближена деяким поліномом
може бути добре наближена деяким поліномом ![]() (див. [1], c.50):
(див. [1], c.50):
Теорема Вейерштрасса: Для будь-якого ![]() існує поліном
існує поліном ![]() степеня
степеня ![]() , такий, що
, такий, що ![]() .
.
Отже, будемо шукати інтерполяційний поліном в вигляді:
![]() , (1. 1. 2)
, (1. 1. 2)
де ![]() - невизначені коефіцієнти. Покладемо
- невизначені коефіцієнти. Покладемо ![]() , тоді отримаємо систему лінійних рівнянь:
, тоді отримаємо систему лінійних рівнянь:

Визначник даної системи являється відмінним від нуля визначником Вандермонда (див. [9]):
 .
.
Звідси випливає, що інтерполяційний поліном (1. 1. 2) існує і він єдиний, хоча форм його запису існує багато.
В якості базису ![]() ми взяли базис із одночленів
ми взяли базис із одночленів ![]() . Для обчислень більш зручним являється базис поліномів Лагранжа
. Для обчислень більш зручним являється базис поліномів Лагранжа ![]() степеня п або коефіцієнтів Лагранжа:
степеня п або коефіцієнтів Лагранжа:

Неважко побачити, що поліном степені п
![]()
задовольняє цим умовам. Полином ![]() , очевидно, визначається єдиним способом. Дійсно, нехай існує ще один поліном
, очевидно, визначається єдиним способом. Дійсно, нехай існує ще один поліном ![]() , тоді їх різниця
, тоді їх різниця ![]() є поліном степені п, який перетворюється в нуль в п+1 точках
є поліном степені п, який перетворюється в нуль в п+1 точках ![]() . Це можливо тільки при
. Це можливо тільки при ![]() .
.
Поліном ![]() приймає значення
приймає значення ![]() в точці
в точці ![]() і рівний нулю у всіх останніх вузлах
і рівний нулю у всіх останніх вузлах ![]() при
при ![]() . Звідси випливає, що інтерполяційний поліном:
. Звідси випливає, що інтерполяційний поліном:
![]() (1. 1. 3)
(1. 1. 3)
має степінь не вище п і ![]() . Формулу (1. 1. 3) називають формулою Лагранжа. Число арифметичних дій для обчислення по (1. 1. 3) пропорційно
. Формулу (1. 1. 3) називають формулою Лагранжа. Число арифметичних дій для обчислення по (1. 1. 3) пропорційно ![]() . Для оцінки близькості полінома
. Для оцінки близькості полінома ![]() до функції
до функції ![]() покладають, що існує п+1– ша неперервна похідна
покладають, що існує п+1– ша неперервна похідна ![]() . Тоді має місце формула для похибки
. Тоді має місце формула для похибки
 .
.
При оцінці похибки результатів повинні враховуватись як похибки методу інтерполяції (залишковий член), так і похибка округлення при обчисленнях.
1.2 Інтерполяційні формули Ньютона
Часто інтерполювання ведеться для функцій, заданих таблицями з рівновіддаленими значеннями аргументу (тобто такими, що будь-який ![]() (вузол інтерполяції) можна представити у вигляді
(вузол інтерполяції) можна представити у вигляді ![]() - деяка постійна величина, яка називається кроком інтерполяції). Для таких таблиць побудова інтерполяційних формул, а також проведення обчислень по ним значно спрощується.
- деяка постійна величина, яка називається кроком інтерполяції). Для таких таблиць побудова інтерполяційних формул, а також проведення обчислень по ним значно спрощується.
Для побудови формули Ньютона необхідно ввести поняття кінцевих різниць.
Кінцевими різницями називають різниці між значеннями функції в сусідніх вузлах (точках ![]() ) інтерполяції:
) інтерполяції:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
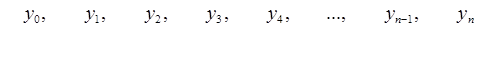
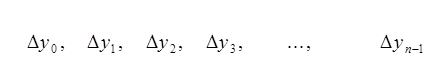
де ![]() Отримані кінцеві різниці будемо називати кінцевими різницями першого порядку. З різниць першого порядку отримаємо різниці другого порядку:
Отримані кінцеві різниці будемо називати кінцевими різницями першого порядку. З різниць першого порядку отримаємо різниці другого порядку: