Курсовая работа: Інтерполювання функцій

Однак, більш важливим для розуміння суті поліноміального інтерполювання є твердження, обернене зробленому вище висновку. А саме, що якщо кінцеві різниці п-го порядку деякої функції постійні в будь-якій точці при різних фіксованих кроках , то ця функція є многочлен степеня п.

Для функції , заданої таблицею своїх значень у вузлах , де , кінцеві різниці різних порядків зручно поміщати в одну загальну таблицю з вузлами і значеннями функції. Цю загальну таблицю називають таблицею кінцевих різниць.

1.2.1 Перша інтерполяційна формула Ньютона

Нехай для функції задані значення для рівновіддалених значень незалежної змінної: , де - крок інтерполяції. Необхідно підібрати поліном степені не вище п, який приймає в точках значення

(1. 2. 3)

Умови (1. 2. 3) еквівалентні тому, що . Слідуючи Ньютону, будемо шукати поліном у вигляді

Використовуючи загальний степінь, вираз (1. 2. 3) запишемо так:

Наша задача заклечається у визначенні коефіцієнтів полінома . Покладаючи у вираз (1. 2. 5), отримаємо .

Щоб знайти коефіцієнт , складемо першу кінцеву різницю . Припускаючи в останньому виразі , отримаємо: ; звідки . Для визначення коефіцієнта складемо кінцеву різницю другого порядку . Покладаючи , отримаємо: ; звідки . Послідовно продовжуючи цей процес, ми виявимо, що , де .

Підставляючи знайдені значення коефіцієнтів у вираз (1. 2. 5) отримаємо інтерполяційний поліном Ньютона

. (1. 2. 6)

Легко побачити, що поліном (1. 2. 6.) повністю задовольняє вимогам поставленої задачі. Дійсно, по-перше, степінь поліному не вище п, по-друге, і

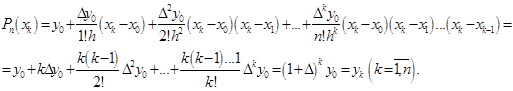
Замітимо, що при формула (1. 2. 6) перетворюється в ряд Тейлора для функції . Дійсно, 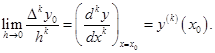Крім того, очевидно, . Звідси при формула (1. 2. 6) приймає вид поліному Тейлора: .

Для практичного використання інтерполяційну формулу Ньютона (1. 2. 6) зазвичай записують в дещо перетвореному вигляді. Для цього введемо нову змінну за формулою ; тоді

підставляючи ці вирази у формулу (1. 2. 6), отримаємо:

, (1. 2. 7)

де являє собою кількість кроків, необхідних для досягнення точки , виходячи із точки . Це і є кінцевий вигляд першої інтерполяційної формули Ньютона.

Формулу (1. 2. 7) вигідно використовувати для інтерполювання функції в околі початкового значення , де мале за абсолютною величиною.

Якщо у формулі (1. 2. 7) покласти п=1, то отримаємо формулу лінійного інтерполювання: . При п=2 будемо мати формулу параболічного або квадратичного інтерполювання

.

Якщо дана необмежена таблиця значень , то число в інтерполяційній формулі (1. 2. 7) може бути довільним. Практично в цьому випадку число обирають так, щоб різниця була постійною із заданою точністю. За початкове значення можна приймати довільне табличне значення аргументу .

Якщо таблиця значень функції скінчена, то - число обмежене, а саме: не може бути більше числа значень функції , зменшеного на одиницю.

Відзначимо, що при застосуванні першої інтерполяційної формули Ньютона зручно використовувати горизонтальну таблицю різниць, так як потрібні значення різниць функції знаходяться у відповідному горизонтальному рядку таблиці.

1.2.2 Друга інтерполяційна формула Ньютона

Перша інтерполяційна формула Ньютона практично незручна для інтерполювання функції поблизу вузлів таблиці. В такому випадку зазвичай застосовують другу інтерполяційну формулу Ньютона. Виведемо цю формулу.