Курсовая работа: Інтерполювання функцій

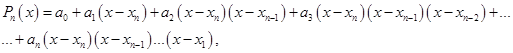
або, використовуючи узагальнену степінь, отримуємо:

. (1. 2. 8)

Наша задача полягає у визначенні коефіцієнтів таким чином, щоб виконувались умови (1. 2. 3). Для цього необхідно і достатньо, щоб

(1. 2. 9)

Покладемо у формулі (1. 2. 8). Тоді будемо мати: , отже .

Далі беремо від лівої і правої формули (1. 2. 8) кінцеві різниці першого порядку

.

Звідси, вважаючи і враховуючи відношення (1. 2. 9) будемо мати:

. Отже .

Покладаючи знаходимо: . І таким чином .

Характер закономірності коефіцієнтів достатньо зрозумілий. Застосовуючи метод математичної індукції, можна строго довести, що

(1. 2. 10)

Підставляючи ці значення у формулу (1. 2. 8) будемо мати остаточно

(1. 2. 11)

Формула (1. 2. 11) носить назву другої інтерполяційної формули Ньютона.

Введемо більш зручний запис формули (1. 2. 11). Нехай , тоді

і т. д.

Підставивши ці значення у формулу (1. 2. 11), отримаємо:

.(1.2.12)

Це і є загальний вигляд другої інтерполяційної формули Ньютона. Для наближеного обчислення значень функції вважають, що .

Як перша, так и друга інтерполяційні формули Ньютона можуть бути використані для екстраполяції, тобто, для знаходження значень функції для значень аргументів , котрі лежать за межами таблиці. Якщо і близько до , то вигідно використовувати першу інтерполяційну формулу Ньютона, причому тоді . Якщо ж і близько до , то зручніше використовувати другу інтерполяційну формулу Ньютона, причому тоді . Таким чином, перша інтерполяційна формула Ньютона використовується для інтерполяції вперед і екстраполяції назад, а друга інтерполяційна формула Ньютона, навпаки, – для інтерполяції назад і екстраполяції вперед (див. [8]).

Відмітимо, що операція екстраполяції, взагалі кажучи, менш точна, ніж операція інтерполяції у вузькому значенні слова.

1.2.3 Оцінка похибок інтерполяційних формул Ньютона

Для функції ми побудували інтерполяційний поліном Ньютона , який приймає в точках задані значення . Виникає питання, наскільки близько побудований поліном наближається до функції в інших точках, тобто наскільки великий залишковий член . Для визначення цього степеня наближення накладемо на функцію додаткові обмеження. А саме, ми будемо припускати, що в області зміни : , котра містить вузли інтерполювання, функція маєвсі похідні до (п+1)-го порядку включаючи.

Введемо допоміжну функцію

, (1.2.12)де і

- постійний коефіцієнт, котрий буде обрано нижче.

Функція , очевидно, має п+1 корінь в точках . Підберемо тепер коефіцієнт таким чином, щоб мала (п+2)-ий корінь в будь-якій, але фіксованій точці відрізка , яка не співпадає з вузлами інтерполювання (мал. 1). Для цього достатньо покласти