Курсовая работа: Інтерполювання функцій

При побудові інтерполяційних формул Ньютона використовуються лише значення функції, що лежать з однієї сторони початкового наближення, тобто, ці формули носять односторонній характер (див.[3]).

В багатьох випадках виявляються корисними інтерполяційні формули, що містять як наступні, так і попередні значення функції по відношенню до її початкового наближеного значення. Найбільш вживаними серед них являються ті, що містять різниці, розміщені у горизонтальному рядку діагональної таблиці різниць даної функції, що відповідає початковим значенням і , або в рядках, що безпосередньо примикають до неї. Ці різниці називаються центральними різницями, причому і т. д.

Відповідні їм формули називають інтерполяційними формулами із центральними різницями. До їх числа відносяться формули Гауса, Стірлінга і Бесселя.

Постановка задачі. Нехай маємо 2п+1 рівновіддалені вузли інтерполяції:

,

де , ідля функції відомі її значення в цих вузлах , потрібно побудувати такий поліном степені не вище 2п, що. Із останньої умови випливає, що

(1. 3. 1)

для всіх відповідних значень і та k.

Будемо шукати поліном у вигляді:

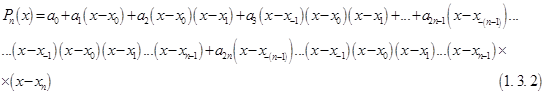
Вводячи узагальнені степені (див [3]), отримаємо:

Застосовуючи для обчислення коефіцієнтів такий ж