Курсовая работа: Инвариантные подгруппы бипримарных групп

3) , 1 и делит порядок .

Теорема. Пусть - группа порядка , и - простые числа. Если , то либо обладает характеристической -подгруппой порядка , либо справедливо одно из следующих утверждений:

1) , , и ;

2) , , , причем , если , и , если ;

3) , , и .

Теорема. Группа порядка , , не имеющая неединичных инвариантных -подгрупп, существует для каждого из следующих трех случаев:

1) , , и ;

2) , , и , если , , если ;

3) , , и .

Теорема. Пусть и - различные простые числа и - порядок силовской -подгруппы из группы . Тогда и только , когда выполняется одно из условий:

1) , , - любое натуральное число за исключением , , , , , , , , , , , , , , , ;

2) , , - любое натуральное число ;

3) , , - любое натуральное число за исключением , где ; , где - любое целое число, удовлетворяющее неравенству 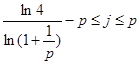. Для дополнительно исключаются числа , , и ; для дополнительно исключаются и .

Завершает мою курсовую работу список используемой литературы, который состоит из девяти источников.

1. Основные обозначения

	группа
	порядок группы
	класс всех разрешимых групп
	класс всех нильпотентных групп
	является подгруппой группы
	является нормальной подгруппой группы
	прямое произведение подгрупп и
	« 1 2 3 4 5 6 » К-во Просмотров: 206 Бесплатно скачать Курсовая работа: Инвариантные подгруппы бипримарных групп >>> Скачать <<< Меню Поиск