Курсовая работа: Инвариантные подгруппы бипримарных групп
3) 
, 
, 
и 
.
2. Порядки силовских подгрупп полных линейных групп. На множестве натуральных чисел введем следующую функцию:
где 
и 
взаимно просто с 
. Из определения вытекает, что 
есть показатель, с которым входит в произведение 
. Поэтому
где 
- целая часть числа 
(см. ) и 
- наибольшее число, при котором 
.
Тогда
Лемма 
.
Лемма Пусть 
- показатель, которому 
принадлежит по модулю 
, и пусть 
, не делит 
. Тогда и только тогда делит 
, когда 
кратно . Если 
, не делит 
, то, за исключением случая 
, число 
есть наивысшая степень , которая делит 
.
Доказательство. Первое утверждение вытекает из свойств показателей (см. (5)). Вычислим 
, используя бином Ньютона:
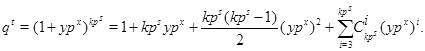
Заметим, что
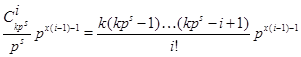
есть целое число. Действительно, 
и число 
делит произведение 
. Учитывая, что 
, из леммы получаем, что 
и 
делит 
. Теперь
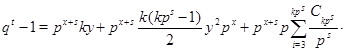
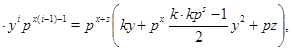
где 
- целое число. Так как не делит 
, то выражение в скобках не делится на , за исключением случая 
. Лемма доказана.
Исключение , в лемме существенно; легко заметить, что при 
, 
лемма неверна. Случай был как раз и пропущен в рассуждениях работы (5).
Лемма Пусть 
, - нечетное число и 
- наименьшее целое число, при котором 
. Пусть 
. Определим число 
так: если, 
, то 
. если 
, тo 
- нечетное число. Тогда
1) если - нечетное число, то 
; 
;
2) если - четное число и 
, - нечетное число, то 
, 
, где 
, 
, 
и 
- нечетные числа.
Доказательство. Воспользуемся биномом Ньютона:
Если - нечетное число, то
- нечетное число. Если - четное число, то
