Курсовая работа: Иррациональные уравнения

Пример 2. Решить уравнение (8).

Решение. Т.к. , то умножим обе части уравнения на выражение , являющееся сопряженным левой части уравнения (8). . После приведения подобных слагаемых получаем уравнение (9), равносильное исходному, т.к. уравнение действительных корней не имеет. Складывая уравнения (8) и (9) получаем, что . Тогда

О т в е т:.

Замечание. Также уравнения вида можно решать с помощью ОДЗ уравнения и равносильных переходов от одних уравнений к другим.

Пример 3. Решить уравнение

Решение. Найдем ОДЗ переменной х.

ОДЗ:Следовательно,

На ОДЗ обе части уравнения положительны, поэтому после возведения в квадрат получим уравнение: , равносильное для уравнению

Иногда решения уравнения можно найти, решая его на разных числовых промежутках.

Для любого имеем , а . Следовательно, среди нет решений уравнения .

Для имеем . Следовательно, для . . Тогда . Т.к. , то является корнем уравнения , равносильному уравнению для этих х.

О т в е т: .

Пример 4. Решить уравнение

Решение. Преобразуем исходное уравнение.

Возведем обе части данного уравнения в квадрат.

Проверка показывает, что 5 является корнем исходного уравнения.

Замечание. Иногда значительно проще можно решать уравнения вида , если воспользоваться свойствами монотонности функций, а именно тем, что сумма двух возрастающих функций является возрастающей функцией, и всякая монотонная функция каждое свое значение принимает, лишь при одном значении аргумента. Действительно, функции и - возрастающие. Следовательно, их сумма - возрастающая функция.

Значит, исходное уравнение, если имеет корень, то только один. В этом случае, учитывая, что , подбором легко найти, что 5 является корнем исходного уравнения.

О т в е т:{5}.

Пример 5. Решить уравнение

Решение. Если обе части исходного уравнения возвести в квадрат, то получится довольно сложное уравнение. Поступим по-другому: преобразуем уравнение к виду:

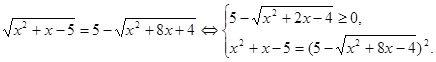
Решим неравенство системы.

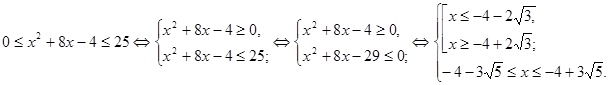
Решением системы является множество:

.

Решим уравнение системы.