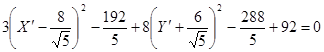Курсовая работа: Исследование кривых и поверхностей второго порядка

Дано:

Определить тип кривой с помощью инвариантов в зависимости от β:

Вычислим инварианты:

1. Если , то имеем линии эллиптического типа

Этих β будет эллипс

При

При

2. Если то пишем линии параболического типа, при этом, чтобы была парабола

3. Если , то получаем линии гиперболического типа.

При гипербола

При корней нет, т.е. таких двух пересекающихся прямых, не существует.

Значение
Тип кривой	Мнимая точка	Точка	Эллипс	Парабола	Гипербола

Исследуем кривую при β=0 , тогда получим:

Сперва повернём на угол φ:

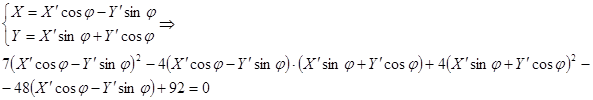
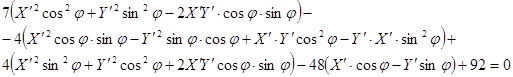
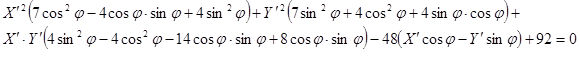
Найдём угол φ,такой чтобы коэффициент при был равен 0:

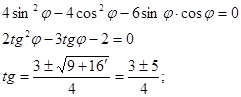
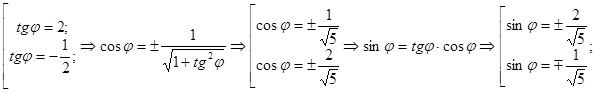
Пусть

Сгруппируем члены уравнения и дополним до полного квадрата: