Курсовая работа: Исследование кривых и поверхностей второго порядка

11) — две мнимые пересекающиеся плоскости (ось

O 'Z ),

12) — гиперболический цилиндр,

13) — две пересекающиеся плоскости,

14) — параболический цилиндр,

15) — две параллельные плоскости,

16) — две мнимые параллельные плоскости,

17) — две совпадающие плоскости (плоскость XOZ ).

В выше перечисленных уравнениях a , b , c , p ­— положительные параметры. Систему координат называют канонической.

Исследование формы поверхности второго порядка методом сечения плоскостями

Если дано каноническое уравнение поверхности S , то представление о поверхности можно получить по форме линий пересечения ее плоскостями:

Z = h — параллельными координатной плоскости XO ' Y ,

X = h — параллельными координатной плоскости YO ' Z ,

Y = h — параллельными координатной плоскости XO ' Z .

Практическая часть

Дано:

;

Это эллипсоид в прямоугольной декартовой системе координат Oxyz, где оси OX, OY, OZ — оси симметрии.

1. Рассмотрим линии плоскостями Z=h (h=const):

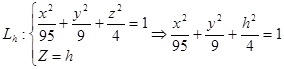(1)

Плоскость Z = h параллельна плоскости Oxy.

Уравнения проекций на Oxy имеют вид:

Если , то , и тогда поделим обе части уравнения на , получим:

Это уравнение эллипсов с полуосями , ; увеличивающиеся с уменьшением , центр эллипса (0;0;h)

При различных h имеем:

Если , тогда и значит линии удовлетворяющих уравнению(1) нет.