Курсовая работа: Изучение плоских диэлектрических волноводов для ТЕ поляризации
![]() (9)
(9)
![]() (10)
(10)
![]() ,
, ![]() (11,12)
(11,12)
Продифференцировав (7) по ![]() , имеем:
, имеем:
![]() (13).
(13).
Учитывая второе уравнение, получаем:
![]() (14)
(14)
Так как ![]() , то
, то ![]() .
.
Отсюда имеем :
![]() (15)
(15)
- это волновое уравнение, описывающее распространение волн со скоростью ![]() .
.
Решение этого уравнения записывается наиболее просто случае, когда ![]() зависит лишь от
зависит лишь от ![]() и
и ![]() .Тогда уравнение сводится к следующему:
.Тогда уравнение сводится к следующему:
 сделаем замену переменных
сделаем замену переменных ![]() и
и ![]() , в соответствии с которой
, в соответствии с которой ![]() ,
, ![]()
![]() получим:
получим:
![]() (16).
(16).
Делаем вывод, что общее решение имеет вид:
![]() , где
, где ![]() и
и ![]() произвольные функции. Это суперпозиция двух возмущений, распространяющихся со скоростью
произвольные функции. Это суперпозиция двух возмущений, распространяющихся со скоростью ![]() .
.
Теперь учтем, что диэлектрическая и магнитная проницаемости – это комплексные величины:
![]() (17)
(17)
![]() (18)
(18)
значит  и
и ![]()
 ,
,
где ![]() ,
, ![]() - вектор плотности электрического тока
- вектор плотности электрического тока ![]() , где
, где ![]() - суммарная плотность объемного заряда в исследуемом объеме. Временную зависимость можно представить в виде экспоненты
- суммарная плотность объемного заряда в исследуемом объеме. Временную зависимость можно представить в виде экспоненты ![]() .Тогда дифференциальные уравнения для E иH примут вид:
.Тогда дифференциальные уравнения для E иH примут вид:


или
![]()
![]() , где
, где ![]() - комплексная диэлектрическая проницаемость, учитывающая эффекты рассеяния.
- комплексная диэлектрическая проницаемость, учитывающая эффекты рассеяния.
Получили еще одно волновое уравнение, в скалярном виде. Его решение будет иметь вид: ![]() , где
, где ![]() - комплексная постоянная распространения, а k – единичный вектор в направлении распространении волны. Действительная часть постоянной распространения представляет собой коэффициент поглощения по амплитуде, а мнимая часть – модуль волнового вектора
- комплексная постоянная распространения, а k – единичный вектор в направлении распространении волны. Действительная часть постоянной распространения представляет собой коэффициент поглощения по амплитуде, а мнимая часть – модуль волнового вектора ![]() .
.
В случае плоской волны векторы E , H , k ортогональны и отношение модулей векторов E , H : 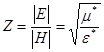 есть характеристический волновой импеданс.
есть характеристический волновой импеданс.
Параметры среды.