Курсовая работа: Изучение плоских диэлектрических волноводов для ТЕ поляризации

Граничные условия.

Исходя из условий Максвелла в интегральной форме, можно определить условия для векторов E , D , H , B на границе раздела двух сред, с разными и .

(19)

(20)

(21)

(22)

Где индексом i обозначены составляющие векторов, касательные к поверхности раздела двух сред 1 и 2. А индексом n – составляющие, нормальные к этой поверхности. Величина J – плотность поверхностных токов проводимости, а - плотность электрических зарядов, причем в тех случаях, которые мы будем рассматривать, они равны нулю. Эти же уравнения можно представить в векторной форме, если ввести в рассмотрение единичный вектор нормали к границе раздела.

Таким образом:

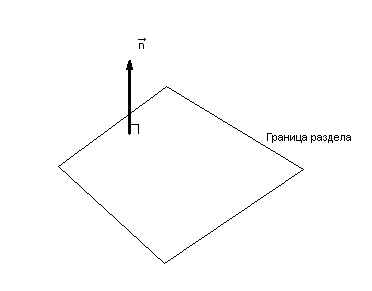
Формулы Френеля.

Пусть А – амплитуда электрического вектора поля падающей волны. Будем считать ее комплексной величиной с фазой , равной постоянной части аргумента волновой функции. Переменная ее часть имеет вид:

Теперь разложим вектор на параллельную и перпендикулярную составляющие:

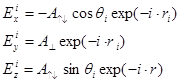
Компоненты магнитного вектора получаются из соотношения

Отсюда

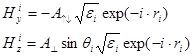
Граничные условия и требуют чтобы на границе тангенциальная составляющие векторов E и H были непрерывны. Следовательно, нужно потребовать выполнения следующих соотношений

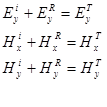
Теперь можно получить важные соотношения (уравнения):

(23)

(24)

(25)

(26)

Решая эти уравнения, получаем уравнения Френеля:

(27)