Курсовая работа: Краевые задачи для алгоритмов приближённого построения заданного режима термообработки проволок на встречных курсах
1. Искомый эффект этой термообработки достигается нагревом проволок до данной максимальной температуры 
, а качество термообработки определяется уровнем возмущений 
температуры , ограниченных определённой предельной величиной [].
2. В интервале температур термообработки материал проволок сохраняет неизменными свои плотность 
и удельную теплоёмкость 
.
3. Теплоизоляция термоаппарата, столь совершенна, что всё тепло, поступающее из внешних источников, поглощается обрабатываемыми проволоками.
4. Тепловая инерция муфеля намного превосходит тепловую инерцию содержащихся в нём проволок.
5. Тепловые потоки между проволоками и муфелем нормальны к его оси Ох и подчиняется закону теплопроводности Фурье, т.е. пропорциональны соответствующим разностям температур.
6. Плотность теплового потока от внешнего источника тепла 
постоянна по длине и ширине муфеля.
Математической моделью данного вида термообработки служат уравнения теплового баланса на участке рабочей зоны [ x , x +∆ x ] за интервал времени ∆t при стационарном термопроцессе.
Пусть ТА =ТА (х), TB =T B ( x ), TC = TC ( x ) – стационарные распределения температур проволок и муфеля в рабочей зоне х
[-L; L]
(1.1)
— их приращения на участке рабочей зоны [х; х+ ∆x],
(1.2)
— количества массы этих проволок, проходящих за время ∆t через данный участок канала,
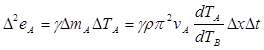(1.3)
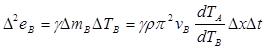(1.4)
– количества тепловой энергии, поглощаемой здесь за это время проволоками А и В,
(1.5)
– среднее количество тепла, поглощаемой одной проволокой на участке рабочей зоны [х; х+∆х] за время ∆t.
При равномерном обогреве муфеля за время ∆t на данном участке канала в расчёте на одну проволоку поступит количества тепла
(1.6)
Из (1.5) и (1.6) находим, что при муфельном нагреве
(1.7)
В то же время, скорости изменения температур проволок равны
(1.8)
а скорость изменения их средней температуры ровна
(1.9)
следовательно,
(1.10)
(1.11)
при чём i=const, если i=const.