Курсовая работа: Краевые задачи для алгоритмов приближённого построения заданного режима термообработки проволок на встречных курсах

(3.8)

Из этой же системы находим закон распределения температуры муфеля:

(3.9)

откуда получим

(3.10)

Находим плотность потока j(x) из системы (3.1) учитывая Т_А =Т^* , (3.8), (3.10).

(3.11)

Пусть теперь на известен закон распределения температуры проволоки А (см. рис1):

(3.12)

И пусть для проволоки В известно начальное условие:

(3.13)

Тогда согласно этому закону и начальному условию находим законы распределения температур проволоки В, муфеля и плотности j.

Учитывая уравнение (3.4) находим Т _B (х)

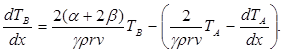(3.14)

(3.14) является линейным неоднородным уравнением вида [4]

(3.15)

Его решением является

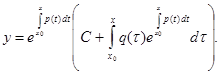(3.16)

Откуда находим

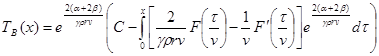. (3.17)

Учитывая начальное условие (3.13) находим С=const

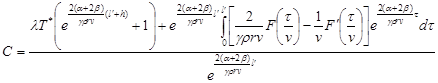(3.18)

Подставляя С в (3.17) находим закон распределения температуры проволоки B:

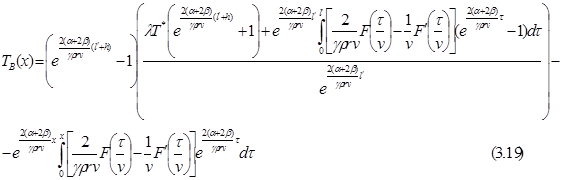
Из (3.9) определим закон распределения температуры муфеля

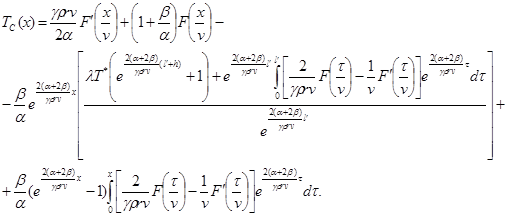(3.20)

Плотность теплового потока j находим из третьего уравнения системы (3.1), учитывая формулы (3.12), (3.19), (3.20).

Согласно второму параграфу на I=[-h; h] плотность потока j₀ постоянная величина. Найдём её.

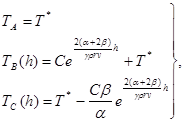(3.21)