Курсовая работа: курсовые
![]() .Все вышеперечисленные условия выполняются, следовательно можно использовать формулу (1.2).
.Все вышеперечисленные условия выполняются, следовательно можно использовать формулу (1.2).
![]() .
.
Получили формулу:
![]() . (
. (![]() ).
).
Пример 2.Получим асимптотическое разложение гамма-функции Эйлера

Метод Лапласа непосредственно неприменим к этому интегралу, так как функция ![]() не имеет максимума на данном интервале.
не имеет максимума на данном интервале.
Представим подинтегральную функцию в виде
![]()
и сделаем замену переменной, положив ![]() .Тогда имеем:
.Тогда имеем:
 .
.
Наш интеграл примет вид:
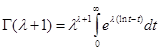 .
.
Это интеграл Лапласа: здесь ![]() и
и ![]() .Функция
.Функция ![]() достигает максимума при
достигает максимума при ![]() , причем
, причем ![]() Поэтому по формуле (1.2) получаем
Поэтому по формуле (1.2) получаем
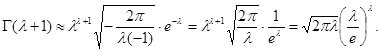
Получили формулу:
![]()
Из этой формулы непосредственно следует формула Стирлинга
![]()
так как ![]() для любого натурального
для любого натурального ![]() .
.
Пусть теперь ![]() совпадает с одним из концов отрезка, например
совпадает с одним из концов отрезка, например ![]() ,и пусть для простоты
,и пусть для простоты ![]() .Заменяя
.Заменяя ![]() интегралом по отрезку
интегралом по отрезку ![]() и заменяя приближенно на этом отрезке функции
и заменяя приближенно на этом отрезке функции
![]()
![]() , получаем,что
, получаем,что
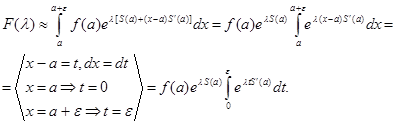
Заметим,что ![]() .Вычисляя последний интеграл,получаем
.Вычисляя последний интеграл,получаем
![]() , (
, (![]() ) (1.3)
) (1.3)
Пример 3.Вычислим интеграл
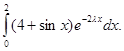
Здесь функция ![]() на отрезке [0,2] имеет максимум в точке
на отрезке [0,2] имеет максимум в точке ![]() ; также
; также
![]() Следовательно, можно применить формулу (1.3):
Следовательно, можно применить формулу (1.3):