Курсовая работа: Линейное программирование как метод оптимизации

Задача ЛП в канонической форме:

(2.1)

(2.2)

(2.3)

Задача ЛП в стандартной форме:

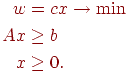
В обоих случаях А есть матрица размерности m x n, i-я строка которой совпадает с вектором а_i .

Задача ЛП в общей форме сводится (в определенном смысле) к задаче ЛП в канонической (стандартной) форме. Под этим понимается существование общего способа построения по исходной задаче (в общей форме) новой задачи ЛП (в нужной нам форме), любое оптимальное решение которой "легко" преобразуется в оптимальное решение исходной задачи и наоборот. (Фактически, связь между этими задачами оказывается еще более тесной). Тем самым мы получаем возможность, не теряя общности, заниматься изучением задач ЛП, представленных либо в канонической, либо в стандартной форме. Ввиду этого наши дальнейшие рассмотрения задач ЛП будут посвящены, главным образом, задачам в канонической форме.

2. Приведение задачи линейного программирования к стандартной форме

Любая задача линейного программирования приводится к стандартной (канонической) форме основной задачи линейного программирования, которая формулируется следующим образом: найти неотрицательные значения переменных X1, X2, Xn, удовлетворяющих ограничениям в виде равенств:

A11X1 + A12X2 + … + A1nXn = B1;

A21X1 + A22X2 + … + A2nXn = B2;

……………………………………

Am1X1 + Am2X2 + … + AmnXn = Bm;

Xj≥ 0, j=1,…,n

и обращающих в максимум линейную функцию этих переменных:

E= C1X1 + C2X2 + … + CnXnÞmax

При этом также требуется, чтобы правые части равенств были неотрицательны, т.е. должны соблюдаться условия:

Bj≥ 0, j=1,…,n

Приведение к стандартной форме необходимо, так как большинство методов решения задач линейного программирования разработано именно для стандартной формы. Для приведения к стандартной форме задачи линейного программирования может потребоваться выполнить следующие действия:

перейти от минимизации целевой функции к ее максимизации;

изменить знаки правых частей ограничений;

перейти от ограничений-неравенств к равенствам;

избавиться от переменных, не имеющих ограничений на знак.

Для решения нашей задачи воспользуемся симплекс-методом, так как этот метод предназначен для решения задач линейного программирования любой размерности.

3. Примеры экономических задач, приводящихся к задачам ЛП

Несмотря на требование линейности функций критериев и ограничений, в рамки линейного программирования попадают многочисленные задачи распределения ресурсов, управления запасами, сетевого и календарного планирования, транспортные задачи и прочие.

Рассмотрим некоторые из них.

Определение оптимального ассортимента. Имеются m видов ресурсов в количествах b1, b2,., b_i , b_m и n видов изделий. Задана матрица A=||a_ij ||, i=1,.,m, j=1,.,n, где a_ij характеризует нормы расхода i-го ресурса на единицу j-го вида изделий. Эффективность производства j-го вида изделий характеризуется показателем C_j , удовлетворяющим условию линейности. Нужно определить такой план выпуска изделий (оптимальный ассортимент), при котором суммарный показатель эффективности будет наибольший.

Обозначим количество единиц k-го вида изделий, выпускаемых предприятием, через x_k , . Тогда математическая модель этой задачи будет иметь такой вид:

(3.1)

при ограничениях

(3.2)

Кроме ограничений на ресурсы (3.2) в эту модель можно ввести дополнительные ограничения на планируемый уровень выпуска продукции , x_i : x_j : x_k = b_i : b_j : b_k для всех i, j, k и т.д.

Оптимальное распределение взаимозаменяемых ресурсов . Имеются m видов взаимозаменяемых ресурсов а₁ , а₂ ,., а_m , используемых при выполнении n различных работ (задач). Объемы работ, которые должны быть выполнены, составляют b₁ , b₂ ,., b_i , b_n единиц. Заданы числа , указывающие, сколько единиц j-й работы можно получить из единицы і-го ресурса, а также C_ij - затраты на производство j-й работы из единицы i-го ресурса. Требуется распределить ресурсы по работам таким образом, чтобы суммарная эффективность выполненных работ была максимальной (или суммарные затраты - минимальными).

Данная задача называется общей распределительной задачей. Количество единиц i-го ресурса, которое выделено на выполнение работ j-го вида, обозначим через x_ij .