Курсовая работа: Линейные и нелинейные электрические цепи постоянного тока

Зарядный ток равен свободной составляющей, т.к ток установившегося режима равен 0 (i_уст =0).

Длительность заряда конденсатора:

t=5τ=5ּ0,5=2,5 с.

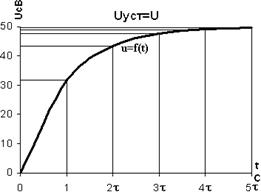
Вычисляем значение напряжения на конденсаторе при его заряде для значений времени t=0, τ, 2τ, 3τ, 4τ, 5τ.

t=0, В;

t=τ, B;

t=2τ, B;

t=3τ, B;

t=4τ, B;

t=5τ, B.

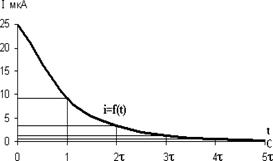
Аналогично вычисляем значения зарядного тока согласно закону изменения переходного тока при заряде конденсатора для значений времени t=0, τ, 2τ, 3τ, 4τ, 5τ.

t, c	0	τ	2τ	3τ	4τ	5τ
i, мкА	25	9, 19	3,38	1,24	0,46	0,17

Согласно полученным результатам строим графики зарядного напряжения и тока в зависимости от τ. (рис 2.7)

рис 2.7

Из построенных графиков u (t) и i (t) можно для любого момента времени определить значение u и i, а также рассчитать запасенную энергию в электрическом поле заряженного конденсатора. Например, при t=3τ:

Дж.

2) Переключатель в положении 2 (разряд конденсатора).

Быстрота разряда конденсатора также зависит от параметров цепи и характеризуется постоянной времени, разряда конденсатора:

τ =RC=10⁴ ּ50ּ10^-6 =0,5 с

На основании второго закона коммутации получены законы, характеризующие напряжение и ток при разряде конденсатора:

где U- напряжение заряженного конденсатора до начала разряда.

Разрядные напряжения и ток равны их свободным составляющим, т.к напряжение и ток установившегося режима после разряда равны 0 (u_{c уст} =0, i_уст =0).

Длительность разряда конденсатора:

t=5τ=0,5ּ5=2,5 с.

Вычисляем значения напряжения конденсатора при его разряде для, значений времени

t=0, τ, 2τ, 3τ, 4τ, 5τ.

t=0, В;