Курсовая работа: Математические методы и модели исследования операций
7 вид продукции (-∞; 2,4762].
Эти интервалы показывают, что при изменении удельной прибыли от продажи единицы одного вида продукции не изменят структуру оптимального плана.
В последней строке таблицы Objective: Function Max. — оптимальное значение целевой функции (в моем случае Function Max. = 2690,2380). В нашем примере мы производили максимизацию. Определив значения управляемых переменных, мы нашли решение поставленной задачи. Прибыль от реализации всей продукции составляет 2690,2380 единиц.
Во второй таблице сводного отчета содержатся следующие сведения об ограничениях задачи:
В первых двух столбцах — номера и названия ограничений.
В столбце Left Hand Side — левые части ограничений, вычисленные при оптимальных значениях переменных. В моей задаче — это количество ресурсов, которое будет израсходовано при оптимальном выпуске продукции.
В столбце Direction — знаки ограничений.
В столбце Right Hand Side — правые части ограничений. В моей задаче — это количество ресурсов, которое мы имеем по условию задачи.
В столбце Slack or Surplus — остатки или избытки, вычисленные по правилу: «правая часть минус левая» для ограничений типа <= или «левая часть минус правая» для ограничений типа >= Они могут показывать, например, величину неиспользованного ресурса (для лимитирующих ограничений, то есть ограничений сверху) или превышение требуемого уровня (для ограничений-требований, то есть ограничений снизу). Если остаток или избыток равен нулю, то соответствующее ограничение является связанным (активным), а соответствующий ресурс — дефицитным (используемым полностью). В противном случае ограничение несвязанное, а ресурс недефицитен. В моем случае все три ресурса являются дефицитными, т.е. используются полностью. Поэтому можно пожелать производителю делать запасы данных ресурсов для безостановочного производства продукции.
В столбце Shadow Price — теневые цены — двойственные оценки, показывающие, на какую величину изменится оптимальное значение целевой функции при увеличении на единицу правой части соответствующего ограничения, тогда как остальные данные неизменны (например, при добавлении единицы соответствующего ресурса). Кроме того, теневая цена — это максимальная цена, которую стоит платить за дополнительное количество дефицитного ресурса, чтобы приобретение было выгодным, или минимальная цена его продажи. Теневая цена отлична от нуля только для связанных ограничений. В общем, по полученным данным я делаю такой вывод что:
1) При увеличении запаса ресурса R1 на одну единицу моя общая выручка увеличится на 1,2857
2) При увеличении запаса ресурса R2 на одну единицу моя общая выручка увеличится на 2,6190
3) При увеличении запаса ресурса R3 на одну единицу моя общая выручка увеличится на 2,4762
В столбцах Allowable Min. RHS и Allowable Мах. RHS — границы интервалов устойчивости, то есть пределы изменения правых частей ограничений (запасов ресурсов), при которых неизменны соответствующие теневые цены и в оптимальном решении сохраняется прежний набор ненулевых переменных (ассортимент продукции). В моем примере такими интервалами будут: для 1-го ресурса — [511,6667; 686,6667], для 2-го — [112,500; 243,7500], для 3-го — [335,000; 597,500]. Это значит, что оптимальный план производимой продукции не изменится до тех пор, пока запасы/параметры конкретного ресурса не выйдут за рамки его ограничений.
После нахождения решения стало доступным меню Results. С его помощью можно узнать, сколько итераций и времени работы процессора потрачено на поиск решения. Было произведено 5 итераций. Задача была решена за 0,015 секунды (см. рис. 4)
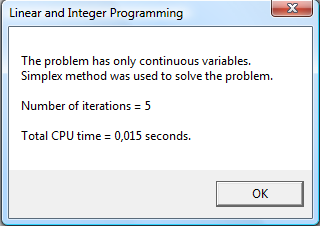
Рис. 4.
После этого была предпринята попытка поиска альтернативного решения, но его не оказалось.
3.2 Графический анализ чувствительности
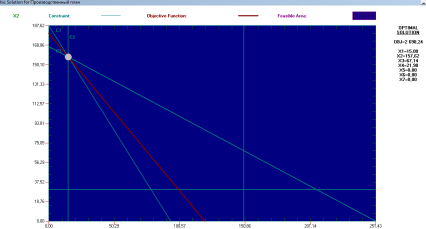
Если выбран графический метод решения, то построенное графическое изображение можно использовать для анализа чувствительности модели. Анализ моделей на чувствительность — это процесс, реализуемый после получения оптимального решения. В рамках такого анализа выявляется чувствительность оптимального решения к определенным изменениям исходной модели.
По оси Х выбран продукт А, по оси У выбран продут В.Я вводила различные изменения параметров и наблюдала за появлением ограничительных линий. С помощью этого метода можно выяснить, как повлияет изменение количества продукции на оптимальное решение. Жирная белая точка показывает пересечение выбранных параметров, текущую оптимальную точку. Вверху графика отмечены следующие обозначения по цветам: принуждённый - constraint; реальный - objective Funkcion; реально выполнимый план на поле - feasible Area (на графике отсутствует).
Заключение
В данной курсовой работе была сформулирована цель работы, построена экономико-математическая модель задачи линейного программирования с её подробным описанием, получен исчерпывающий отчёт о результатах решения задачи, а также получено графическое решение. Всё это осуществлялось при помощи ППП WinQSB, который является на данный момент одним из основных и самых удобных пакетов реализующих большинство математических методов применяемых в экономике и менеджменте.
Итак, я получил оптимальное решения выпуска продукции при максимальной прибыли в 2690,2380 единиц.
Все необходимые ограничения были выполнены. Были выявлены в каком количестве стоит производить продукцию.
Ценность решения задачи линейного программирования в среде WinQSB объясняется возможностью на основании итогового отчёта принимать важные управленческие решения и моделировать реальную производственную ситуацию. Это особенно ценно сейчас, в век широкого применения информационных технологий при решении реальных задач.
Таким образом, было наглядно представлено и прокомментировано полученное решение задачи и нахождение оптимального плана выпуска продукции, где достигалась максимальная прибыль и ресурсы использовались наиболее полно.