Курсовая работа: Математическое моделирование и оптимизация системы массового обслуживания

Пользуясь общими правилами, можно составить уравнения Колмогорова для вероятностей состояний:

(1)

Уравнения (1) называются уравнениями Эрланга. Естественными начальными условиями для их решения являются:

p₀ (0)=1; p₁ (0)=p₂ (0)=...=p_n (0)=0 (в начальный момент система свободна).

Интегрирование системы уравнений (1) в аналитическом виде довольно сложно; на практике такие системы дифференциальных уравнений обычно решаются численно, на ЭВМ. Такое решение дает нам все вероятности состояний p₀ (t), p₁ (t),..., p_n (t) как функции времени.

Естественно, нас больше всего будут интересовать предельные вероятности состояний p₀ , p₁ ,..., p_k ,..., p_n , характеризующие установившийся режим работы СМО (при t ® ¥). Для нахождения предельных вероятностей воспользуемся уже готовым решением задачи, полученным для схемы гибели и размножения. Согласно этому решению,

(2)

В этих формулах интенсивность потока заявок l и интенсивность потока обслуживаний (для одного канала) m не фигурируют по отдельности, а входят только своим отношением l /m. Обозначим это отношение l /m=r и будем называть величину r "приведенной интенсивностью" потока заявок. Физический смысл ее таков: величина r представляет собой среднее число заявок, приходящих в СМО за среднее время обслуживания одной заявки.

С учетом этого обозначения, формулы (2) примут вид:

(3)

Формулы (3) называются формулами Эрланга. Они выражают предельные вероятности всех состояний системы в зависимости от параметров l, m и n (l - интенсивность потока заявок, m - интенсивность обслуживания, n - число каналов СМО).

Зная все вероятности состояний p₀ , p₁ ,..., p_k ,..., p_n , можно найти характеристики эффективности СМО: относительную пропускную способность q, абсолютную пропускную способность А и вероятность отказа P_отк .

Действительно, заявка получает отказ, если приходит в момент, когда все n каналов заняты. Вероятность этого равна

(4)

Вероятность того, что заявка будет принята к обслуживанию (она же относительная пропускная способность q) дополняет P_отк до единицы:

(5)

Абсолютная пропускная способность:

(6)

Одной из важных характеристик СМО с отказами является среднее число занятых каналов (в данном случае оно совпадает со средним числом заявок, находящихся в системе). Обозначим это среднее число k^- .

Величину k^- можно вычислить непосредственно через вероятности p₀ , p₁ ,..., p_n по формуле:

(7)

как математическое ожидание дискретной случайной величины, принимающей значения 0,1,...,n с вероятностями p₀ , p₁ ,..., p_n . однако значительно проще выразить среднее число занятых каналов через абсолютную пропускную способность А, которую мы уже знаем. Действительно, А есть не что иное, как среднее число заявок, обслуживаемых в единицу времени; один занятый канал обслуживает в среднем за единицу времени m заявок; среднее число занятых каналов получится делением А на m:

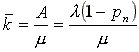или, переходя к обозначению l/m = r,

(8)

[5], [6].

Цель данной работы заключается в разработке модели, имитирующей работу поста ГИБДД. Такая задача была поставлена для того, чтобы выявить эффективность работы системы обслуживания поста ГИБДД для дальнейшей ее оптимизации.

В данной работе предлагается к использованию одна из методик, которая предполагает разделение процесса моделирования на две части. Первая часть –обеспечивает нахождение параметров работы исходной задачи. Вторая часть – производится оптимизация определенных параметров при неизменных остальных параметров в таблицах MS Excel. Строятся графики функций. Производится их анализ и делаются выводы.

Рассмотрим подробнее математическую модель работы поста ГИБДД как системы массового обслуживания. Для решения задачи было принято допущение, что очередь клиентов ограничена, и, следовательно, данная модель является СМО с ограниченной очередью, где n – количество каналов обслуживания. Также принимаем допущение, что все потоки событий (случайные события) в системе являются Марковскими. Напомним, что случайный процесс, протекающий в системе, называется Марковским, если для любого момента времени t0 вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент t0 и не зависят от того, когда и как система пришла в это состояние.

Поток нарушителей в систему поступают с интенсивностью . Тогда

Вероятность отказа .

Относительная пропускная способность .

Абсолютная пропускная способность .

Среднее число заявок, связанных с системой .

Средняя длина очереди .

Количество, ожидающих в очереди .

Время в очереди .

Время в системе .