Курсовая работа: Математическое моделирование и оптимизация системы массового обслуживания

На шоссе проверяет скорость пост ГИБДД. На посту в течении дня работает 5 инспекторов. Рабочий день инспектора равен 10 часам. Режим работы – раз в трое суток. Затраты на одного инспектора равны 35000рублей в месяц (зарплата, налоги, спецобмундирование и др.). Инспектор оформляет протокол примерно за 12 минут. В течение часа скоростной режим нарушают в среднем 35 водителей. Инспекторы останавливают машину, если ожидают оформления не более четырех машин. Средний размер штрафа равен 250 рублям.

Определить параметры работы системы. Найти процент оштрафованных нарушителей. Каково среднее время, которое тратит водитель в ожидании оформления протокола? Сколько, в среднем, машин ожидает оформления? Какова средняя сумма от штрафов за месяц? Каковы месячные затраты на пост ДПС? Определить «прибыль» поста за месяц. (Ознакомительная задача).

Определить оптимальное (с точки зрения прибыли) число инспекторов на посту при сохранении остальных условий задачи.

Имеется возможность арендовать оборудование, позволяющее ускорить процесс оформления протокола. Стоимость аренды оборудования для одного инспектора линейно зависит от его эффективности и изображения на графике. Максимально возможная скорость – 10 протоколов в час. Определить оптимальные затраты на оборудование при неизменных остальных условиях задачи (число инспекторов равно пяти) и при числе инспекторов, полученных в п. 2. Определить параметры работы системы при этих затратах.

Рис. 2.

Провести оптимизацию по двум параметрам: числу инспекторов и затратам на ускоряющее оборудование. Определить параметры работы системы при паре оптимальных параметров. Сравнить с оптимизацией по каждому отдельному параметру.

РЕШЕНИЕ ЗАДАЧИ

Формализуем задачу.

Данную задачу можно отнести к задачам СМО с ограниченной очередью. Максимальная длина очереди равна m =5 . Интенсивность потока требований (в качестве которого выступает поток нарушителей) равна водителей в час. Исходно имеется пять каналов обслуживания (пять инспекторов находятся на посту единовременно): n =5 . Среднее время обслуживания одним каналом (среднее время, которое тратит инспектор на один автомобиль) равно , тогда авт./мин авт./час.

Найдем параметры работы исходной задачи.

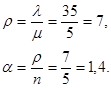
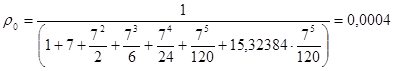
30,4 % нарушителей не будет оштрафовано.

Процент оштрафованных нарушителей равен 69,6 %.

В среднем 24,35 автомобилей будет оштрафовано в час.

Почти все инспекторы (4,8 из 5)заняты.

Найдем среднюю длину очереди:

В среднем ожидает оформления 3 машины.

Время в очереди и системе:

часа = 7,2 мин .

Таким образом, среднее время, которое тратит водитель в ожидании оформления протокола, равно 7,2 мин.

Найдем среднюю сумму штрафов за месяц . Так как авт./час., сумма штрафа в среднем равна 250 руб., в месяце 30 дней по 10 рабочих часов, то: