Курсовая работа: Математическое моделирование и оптимизация системы массового обслуживания
Так как затраты на одного инспектора равны f =35000 руб./мес., а инспекторов по трижды по 5 человек, то месячные затраты на пост ДПС равны:
руб. = 525 тыс. руб .
«Прибыль» поста складывается из суммы штрафов («дохода») минус затраты на инспекторов («расхода»). Таким образом, месячная «прибыль» поста равна:
тыс.руб.
Определить оптимальное число инспекторов можно двумя способами. Во-первых, вручную вычислить все интересующие величины. Во-вторых, все величины можно вычислить в пакете MSExcel.
Составим таблицу 1. В строках 1-5 записаны исходные данные задачи. В столбце А с 10-й по 24-ую строку введены числа инспекторов.
Таблица 1.
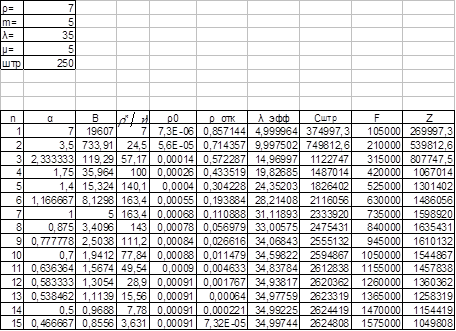
В последнем столбце получено значение прибыли поста за месяц. Построим график этой величины в зависимости от числа инспекторов (рис.3). Тип диаграммы – точечная.
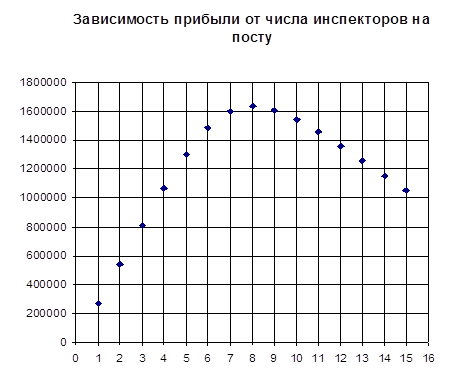
Рис. 3.
Из графика и по значениям в таблице 1 видно, что максимальная прибыль достигается при значении n =8 и равна 1635431 руб. в месяц.
Вывод: При прочих постоянных параметрах, выгоднее нанять 24 инспектора (по 8 инспекторов одновременно).
Определим оптимальные капиталовложения на ускорение оформления протоколов при пяти инспекторах. Требуется формализовать задачу.
Как видно из графика (рис.2), стоимость аренды оборудования для одного инспектора (будем ее обозначать R ) линейно зависит от скорости оформления протокола (интенсивности 
), т.е.
.
Найдем значения параметров R 0 и R 1 . При 
авт./час R =0 . При 
авт./час R =2000 руб./день. Тогда:
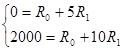
Откуда получаем:
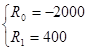
Т.о.
.
При этом 
Оказывается удобнее выразить затраты на аренду через 
, потому что все формулы содержат именно этот параметр. Так как 
авт./час, то
и следовательно
. (1)
При этом
Месячная «прибыль» поста в этом случае будет вычисляться по формуле:
(2)
При n =5 получаем:
(руб./мес.). (3)