Курсовая работа: Методы расчета линейных электрических цепей при импульсном воздействии. Спектральный анализ сигналов

Так как при любом p, то

2. Напряжение .

Так как полученные корни характеристического уравнения являются комплексными сопряженными, то представляет собой затухающий колебательный процесс и ищется как функция вида , где A и ψ – постоянные интегрирования, а δ – декремент затухания. Все эти константы находятся из следующих условий:

Тогда

(рассчитано при проведении качественного анализа)

Так как , то . Решая это уравнение, получим значение константы А:

В результате получаем формулу для переходного напряжения на конденсаторе:

Расчет переходного процесса операторным методом

Суть операторного метода заключается в том, что каждому числу из области функций действительной переменной t ставится во взаимнооднозначное соответствие с помощью операторного отображения по Лапласу некоторое число в области функций комплексной переменной частоты ω. В дифференциальное уравнение или интегро-дифференциальное уравнения функции времени заменяется алгебраическим уравнением в функции частоты.

Операции в области отображений осуществляются с помощью простых алгебраических преобразований, а полученные результаты и помощью отображения Лапласа переводятся в область функций времени.

Отображением по Лапласу называется функция, которая получается в результате следующего интегрирования:

, где

Операторная схема замещения индуктивности содержит операторное сопротивление pL и источник ЭДС . Направление источника совпадает с направлением тока в цепи.

Операторная схема замещения емкости содержит операторное сопротивление и источник ЭДС , напряжение которого противоположно исходному напряжению на емкости.

Все источники заменяются своими операторными отображениями.

Сделав все необходимые преобразования, получаем

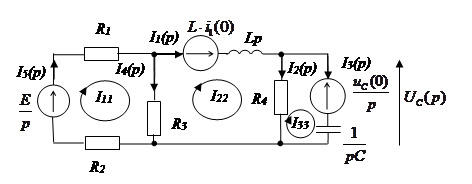
Дерево графа цепи:

Составим систему из трех уравнений по методу контурных токов:

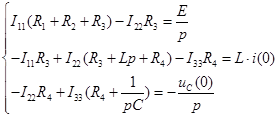
Решим эту систему: