Курсовая работа: Методы расчета линейных электрических цепей при импульсном воздействии. Спектральный анализ сигналов

Переходной характеристикой цепи называется реакция участка цепи или всей цепи на воздействие согнала постоянной единичной величины.

Переходные характеристики удобно вычислять в операторной форме, используя выражение передаточной функции соответствующего вида.

Таким образом переходная функция по напряжению k(t) – закон изменения напряжения на зажимах некоторого участка цепи при подключении к источнику постоянной ЭДС в 1В при нулевых начальных условиях и отсутствии других источников.

Отображение по Лапласу переходной функции по напряжению можно найти, используя формулу

Чтобы найти оригинал данного отображения воспользуемся теоремой разложения Хевисайда. Для этого определим корни знаменателя:

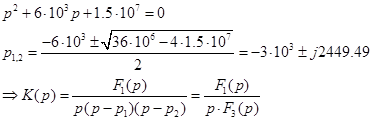
Так как в данном случае два корня комплексные сопряженные, а третий равен 0, то

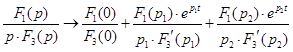, где

Таким образом переходная функция по напряжению равна

Расчет закона изменения искомой величины при подаче на вход цепи импульса заданной формы

Если на цепь воздействует сигнал произвольной формы, то необходимо разбить воздействие на отдельные участки, для которых может быть определен временной скачек, и рассматривать реакцию цепи в виде суммы участков на основании принципа наложения.

Для расчета реакции цепи на каждом участке используется интеграл Дюамеля:

Если воздействие имеет сложную форму, имеет скачи тока или напряжения, то интервал интегрирования разбивается на отдельные участки, и реакция цепи определяется для отдельных участков. При этом результаты не суммируются, а описываются для отдельных участков.

Для того, чтобы применить интеграл Дюамеля, необходимо определить закон изменения входного сигнала на каждом участке:

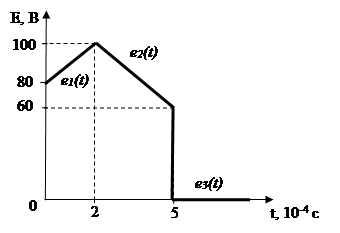
1.

2.

3.

Таким образом