Курсовая работа: Методы расчета цифровых БИХ-фильтров и вид целевой функции

Каскадной схеме соответствует разложение передаточной функции (4) на множители типа

(8)

Реализация рекурсивного фильтра в параллельной форме соответствует представлению передаточной функции (4) в виде суммы простых дробей:

(9)

Это выражение соответствует случаю отсутствия кратных корней в правой части (4). Каждое слагаемое реализуется в виде биквадратных блоков. Все эти блоки соединяются параллельно. Если же есть кратные корни, то может понабиться последовательное соединение биквадратных звеньев для кратных корней.

2. Структурная схема БИХ-фильтра

Исходя из технического задания необходимо привести структурную схему фильтра в каноническом виде и в виде последовательного соединения звеньев первого и второго порядка.

Каноническая форма реализации рекурсивного фильтра выглядит следующим образом:

Форма реализации рекурсивного фильтра в виде последовательного соединения звеньев первого и второго порядка представлена на следующем рисунке:

3. Методы расчета БИХ-фильтров и вид целевой функции

Расчет БИХ-фильтров можно вести в частотной и временной областях. При расчете в частотной области используется синтез по аналоговому и цифровому прототипам. Численные методы расчета разработаны для применения в частотной и временной областях.

Синтез по аналоговому прототипу основан на преобразовании p -плоскости в z -плоскость, а характеристик и параметров аналоговых фильтров - в соответствующие характеристики и параметры цифровых фильтров. Передаточная функция аналогового фильтра на p -плоскости в общем виде может быть записана так:

. (1)

Для перехода к функции и разностному уравнению ЦФ существуют следующие четыре метода.

Метод 1. Отображение дифференциалов. Это наиболее простой метод, сущность которого заключается в замене дифференциалов на конечные разности. В операторном уравнении (1), если дифференциалы заменяются прямыми разностями, то

или ,

а если обратными, то

или .

Недостатком метода является неполное соответствие частотно-избирательных свойств ЦФ свойствам аналогового прототипа. Кроме того, при использовании прямых разностей устойчивый аналоговый фильтр - прототип отображается в неустойчивый ЦФ. Поэтому, несмотря на простоту, применять этот метод не рекомендуется.

Метод 2. Инвариантное преобразование импульсной характеристики (стандартное Z -преобразование). Сущность метода заключается в расчете импульсной характеристики (ИХ) ЦФ по аналоговому прототипу и вычислении системной (передаточной) функции ЦФ.

Достоинством данного метода является подобие импульсных характеристик ЦФ и аналогового прототипа; простота. Недостатком же является наличие эффекта наложения частотных характеристик ЦФ, если полоса пропускания аналогового прототипа превышает . Поэтому точность расчетов ЦФ по данному методу тем выше, чем меньше отношение , где - верхняя частота полосы пропускания ЦФ; - частота дискретизации.

Метод 3. Согласованное Z -преобразование. Полюсы и нули аналогового прототипа на p -плоскости отображаются в полюсы и нули ЦФ на z -плоскости по правилу:

.

Для реализации этого метода передаточную функцию аналогового прототипа представляют в виде произведения сомножителей

,

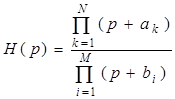где , - действительные или комплексно-сопряженные коэффициенты. Метод согласованного Z -преобразования не применим, если передаточная функция аналогового прототипа имеет только полюсы (нули расположены в бесконечности). Для устранения этого недостатка при расчетах фильтров с нулями в бесконечности рекомендуется вводить полюс того же порядка, что и нуль, в точке .

Метод 4. Билинейное (дробно-линейное) Z -преобразование. При отображении p -плоскости в z -плоскость вся мнимая ось , отображается в единичную окружность. Для этого необходимо выбирать нелинейную монотонную функцию частоты. Эта функция должна изменяться в пределах от до на оси частот дискретизации при изменении от до . В качестве такой функции комплексных частот можно выбрать гиперболический тангенс

или , (2)

которому при соответствует обычный тангенс

.