Курсовая работа: Методы расчета цифровых БИХ-фильтров и вид целевой функции

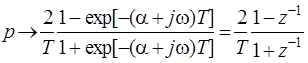. (3)

Таким образом, комплексная плоскость p преобразуется в комплексную z -плоскость заменой переменных (3).

С помощью билинейных Z -преобразований можно от аналогового ФНЧ - прототипа перейти к ЦФ нижних частот (НЧ), верхних частот (ВЧ), полосовому, режекторному, гребенчатому и др.

Билинейное Z -преобразование обладает следующими достоинствами: во-первых, физически реализуемый и устойчивый аналоговый фильтр отображается в физически реализуемый и устойчивый ЦФ: во-вторых, отсутствуют проблемы, связанные с наложениями: в-третьих, нелинейность шкалы частот ЦФ, преобразованного из прототипа, можно учесть для широкого класса фильтров.

Недостатком этого метода является не совпадение импульсной и фазовой характеристик рассчитанного прототипа, поэтому необходимо вводить корректоры и усложнять конструкцию ЦФ. Тем не менее метод билинейного Z -преобразования является самым распространенным аналитическим методом расчета ЦФ.

Для синтеза БИХ ЦФ по цифровому прототипу используются преобразования ЦФ НЧ с безразмерной частотой среза в ЦФ НЧ с другой частотой среза, ЦФ ВЧ, полосовой, режекторный или гребенчатый фильтры. Методика расчета по цифровому прототипу проще, чем методика расчета по аналоговому прототипу, так как в ней отсутствует этап перехода от аналогового фильтра - прототипа к ЦФ.

Применение методов оптимизации для расчета БИХ-фильтров .

В последние годы широкое распространение получил другой класс методов расчета БИХ-фильтров, называемых методами оптимизации. Отличительной чертой этих методов является то, что система уравнений, составленная относительно коэффициентов фильтра, не может быть решена в явной форме. Поэтому для нахождения коэффициентов приходится использовать численные методы оптимизации, минимизирующие, согласно выбранному критерию, некоторую ошибку.

В качестве такого критерия используется критерий минимума среднеквадратической ошибки. При этом целевая функция задачи имеет вид

,

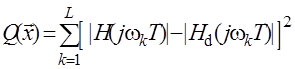где - ()-мерный вектор искомых коэффициентов, - получаемая амплитудная характеристика фильтра, - заданная амплитудная характеристика фильтра, , - дискретный ряд частот, на которых вычисляются отклонения получаемой и заданной характеристик фильтра.

Минимизация функции сводится к нахождению оптимального значения параметрического вектора весовых коэффициентов фильтра . Так как функция является нелинейной, для ее минимизации необходимо использовать эффективные методы оптимизации.

При использовании методов оптимизации учитывается поведение только амплитудной характеристики, поэтому некоторые полюсы или нули после завершения итераций могут оказаться за пределами единичного круга. В этом случае можно прежде всего заменить полюс с полярными координатами , оказавшийся вне единичного круга, на полюс с координатами , находящийся внутри единичного круга. Амплитудная характеристика фильтра при такой замене остается неизменной, так как полюс заменяется своим зеркальным отображением. После того, как все полюсы оказываются внутри единичного круга, появляется возможность с помощью дополнительного анализа еще больше оптимизировать квадрат ошибки. Такая ситуация возникает достаточно часто, и в этих случаях оптимизация должна производиться двумя этапами:

1. Использование программы оптимизации для минимизации функции без каких-либо ограничений на расположение нулей и полюсов.

2. После завершения итераций инвертирование всех полюсов и нулей, оказавшихся вне единичного круга. После этого продолжение оптимизации для нахождения нового минимума .

4. Описание метода синтеза фильтра

При разработке современных систем (в том числе и цифровых фильтров) возникает задача оптимального проектирования. Под этим термином понимается процесс разработки наилучшего, оптимального устройства (в каком-то смысле), как правило с помощью ЭВМ. Большинство методов оптимизации являются итерационными по своей природе.

Как было уже сказано, большинство методов оптимизации, в том числе и методов безусловной оптимизации, носит итерационный характер. Это значит, что начиная с какой-либо точки х₀ , называемой начальным приближением, алгоритм оптимизации генерирует последовательность точек х₁ , х₂ ,…х_n , которая в принципе должна сходиться к точке . На практике процесс генерирования точек прекращается после конечного S числа шагов. И точка выдается в качестве приближения к точке . При этом вычисление очередной точки называется к-той итерацией, а точку - к-ым приближением.

Вектор называется к-тым шагом. Отсюда , к=0,1,2…

В основу всех методов оптимизации положено следующее правило: значение целевой функции от итерации к итерации должно убывать. То есть должно выполняться следующее условие:

Данное условие называется условием спуска.

Методы оптимизации, которые удовлетворяют этому условию, называются допустимыми или методами спуска. Основу всех методов спуска составляет следующая модельная схема:

1. к=0, выбирается начальное приближение ;

2. Проверяются критерий останова. Если критерий выполняется, то расчеты прекращаются и точка выдается как приближение . В противном случае осуществляется переход к следующему пункту.

3. Рассчитывается ненулевой n-мерный вектор , называемый направлением поиска или направлением шага.

4. Вычисляется малое положительное число (длина шага) такое, что должно выполняться условие спуска:

5. Выполнение к-той итерации , к=к+1 и происходит переход к пункту 2.

Шаг 4 в модельной схеме предполагает решение задачи одномерной минимизации – нахождение длины шага h_k . Чтобы решить эту задачу, необходимо, чтобы вектор был допустимым направлением поиска или направлением спуска, условием чего является следующее выражение : , то есть угол между вектором-градиентом и направлением поиска должен быть тупым.

В модельной схеме значение целевой функции F(x) убывает от итерации к итерации. Тем не менее монотонно убывающая последовательность {F(x)} может не сойтись к минимуму по следующим причинам: