Курсовая работа: Межа послідовності. Теорема Штольца

(геометрична прогресія)

Змінний член тієї або іншої прогресії є варіанта.

У зв'язку з визначенням довжини окружності звичайно розглядається периметр правильного вписаного в окружність багатокутника, одержуваного із шестикутника послідовним подвоєнням числа сторін. Таким чином, ця варіанта приймає послідовність значень:

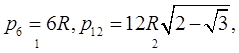
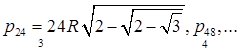
Згадаємо ще про десяткове наближення (по недоліку) до , із всі зростаючою точністю. Воно приймає послідовність значень:

і також представляє варіанту.

Змінну x, що пробігає послідовність (1), часто позначають через , ототожнюючи її зі змінним («загальним») членом цієї послідовності.

Іноді варіанта x_п задається тим, що вказує безпосередньо вираження для x_п ; так, у випадку арифметичної або геометричної прогресії маємо, відповідно, x_п =а+(n-1) d або x_п =aq^n-1 . Користуючись цим вираженням, можна відразу обчислювати будь-яке значення варіанти по заданому його номері, не обчислюючи попередніх значень.

Для периметра правильного вписаного багатокутника таке загальне вираження можливо лише, якщо ввести число π; взагалі периметр р_m правильного вписаного m-косинця дається формулою

1.Межа послідовності

Визначення 1: Числова послідовність {х_п } називається обмеженої зверху (знизу), якщо існує таке число М (т) , що для будь-якого елемента цієї послідовності має місце нерівність , при цьому число М (т) називають верхньою (нижньої) гранню .

Визначення 2: Числова послідовність {х_п } називається обмеженої, якщо вона обмежена й зверху, і знизу, тобто існують М, т, що для будь-якого

Позначимо А = max {|M|, |m|}, тоді очевидно, що числова послідовність буде обмежена, якщо для кожного виконується рівність |x_n |≤А, остання нерівність є умова обмеженості числової послідовності.

Визначення 3: числова послідовність називається нескінченно великою послідовністю, якщо для будь-якого А>0, можна вказати такий номер N, що для всіх n>N виконується | |>A.

Визначення 4: числова послідовність {α_n } називається нескінченно малою послідовністю, якщо для кожного наперед заданого ε > 0, можна вказати такий номер N(ε), що для будь-якого n > N(ε) буде виконуватися нерівність | α_n | < ε.

Визначення 5: числова послідовність {х_п } називається збіжної , якщо існує таке число а, що послідовність {х_п – а} є нескінченно малою послідовністю. При цьому саме а – межа вихідної числової послідовності.

Із цього визначення треба, що все безконечно малі послідовності є збіжними й межу цих послідовностей = 0.

У зв'язку з тим, що поняття збіжної послідовності вв'язано з поняттям нескінченно малої послідовності, то визначення збіжної послідовності можна дати в іншій формі:

Визначення 6: числова послідовність {х_п } називається збіжної до числа а, якщо для будь-якого як завгодно малого найдеться такий , що для всіх n > N виконується нерівність

при ,

а - межа послідовності

Так як рівносильне , а це означає приналежність інтервалу х_n є (a – ε; a+ ?) або, що т же саме, належить ? - околиці крапки а. Тоді ми можемо дати ще одне визначення збіжної числової послідовності.