Курсовая работа: Межа послідовності. Теорема Штольца

Якщо послідовності {x_n } і {у_n } сходяться, то й послідовність {x_n * у_n } також сходиться і її межа дорівнює добутку її множників (меж).

Доказ:

x_n → a, отже x_n = a + α_n

у_n → b, отже у_n = b + β_n

x_n * у_n = (а + α_n )*(b + β_n) =аb+(а β_n + bα_n + α_n β_n )

позначимо γ_n = а β_n + bα_n + α_n β_n , де γ_n елемент нескінченно малої послідовності, виходить

x_n * у_n = ab+ γ_n,

отже,

Теорема 5:

Якщо послідовності {x_n } і {у_n } сходяться до чисел а й b відповідно, і якщо b ≠ 0, межа частки існує, кінцевий і дорівнює частці меж.

Доказ:

Так як послідовність {у_n } сходиться до b, те по визначенню збіжної послідовності, для будь-якого ε > 0, найдеться N(ε), такий що для всіх n > N, буде виконаються нерівність |b – y_n |< ε.

Тоді поклавши , бачимо, що

,

звідки треба

отже

.

Так як, відповідно до умови b ≠ 0, то з останньої нерівності треба, що для всіх n > N елементи послідовності {у_n } не рівні 0, значить саме із цього номера N можна визначити послідовність

x_n = a + α_n

у_n = b + β_n, отже

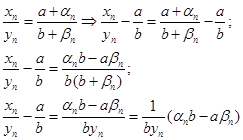
позначимо γ_n = α_п b – aβ_n , γ_n елемент нескінченно малої послідовності.

,

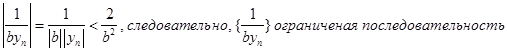а тоді з останньої рівності, треба

,

звідки