Курсовая работа: Моделирование и прогнозирование естественного прироста населения в РФ

Проверим условие равенства нулю суммы значений скорректированной сезонной компоненты:

-20480,000 + 92,000 - 10291,958 - 6639,813 - 11262,333 - 355,333 + 13869,083 + 17015,208 + 14070,708 + 5001,646 - 142,500 - 876,708 = 0

Таким образом получены следующие значения скорректированной сезонной компоненты (Таблица 2):

Таблица 2 - Значения скорректированной сезонной компоненты

Январь	S1	-20480,000	Июль	S7	13869,083
Февраль	S2	92,000	Август	S8	17015,208
Март	S3	-10291,958	Сентябрь	S9	14070,708
Апрель	S4	-6639,813	Октябрь	S10	5001,646
Май	S5	-11262,333	Ноябрь	S11	-142,500
Июнь	S6	-355,333	Декабрь	S12	-876,708

Занесем полученные значения для соответствующих месяцев каждого года.

Шаг 3. Элиминируем влияние скорректированной сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим: T + E = Y – S. Эти значения рассчитываются для каждого момента времени и содержат только тенденцию и случайную компоненту.

Шаг 4. Определим компоненту T данной модели. Для этого проведем аналитическое выравнивание ряда (T + E) с помощью линейного тренда. Результаты выравнивания следующие:

T = -63923,013 + 1156,975 ·t; R ² = 0,889

Таблица 3 - Статистика уравнения тренда

Коэффициенты	Стандартная ошибка	t-статистика	P-Значение
Y-пересечение	-63923,013	1487,618	-42,970	3,23251E-31
t	1156,975	70,114	16,501	8,46925E-18

Уравнение описывает на 88,9% вариацию исходного показателя естественного прироста, при этом уравнение является статистически значимым при уровне надежности 95%.

Подставляя в это уравнение значения t = 1,…, 36, найдем уровни T для каждого момента времени.

Шаг 5. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням T значения сезонной компоненты для соответствующих месяцев.

Шаг 6. В соответствие с методикой построения аддитивной модели расчет абсолютной ошибки производится по формуле:

E = Y – (T + S).

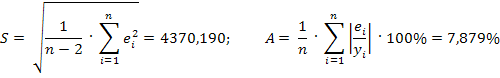
Исходя из значений выше приведенных показателей качества, можно сделать вывод о том, что модель обладает высокой точностью и пригодна для прогнозирования.

2.3 Мультипликативная модель временного ряда

Шаг 1. Проведем выравнивание исходных уровней временного ряда методом простой скользящей средней. Методика, применяемая для мультипликативной модели, полностью совпадает с методикой аддитивной модели. Расчетная таблица модели приведена в Приложении 4.

Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние. Используем эти оценки для расчета значений скорректированной сезонной компоненты. Для этого найдем средние за каждый месяц оценки сезонной компоненты. Взаимопогашаемость сезонных воздействий в мультипликативной модели выражается в том, что сумма значений скорректированной сезонной компоненты по всем кварталам должна быть равно числу периодов в цикле, т.е. двенадцати, так как в нашем случае число периодов одного цикла равно 12 месяцам. В результате имеем следующие сезонные компоненты: 1,526 + 1,010 + 1,280 + 1,183 + 1,329 + 1,032 + 0,712 + 0,631 + 0,680 + 0,874 + 1,008 + 1,021 = 12,287.

Определим скорректированные значения сезонной компоненты, умножив ее на средние оценки на корректирующий коэффициент k:

Проверим условие равенства двенадцати суммы значений скорректированной сезонной компоненты:

1,491 + 0,987 + 1,250 + 1,155 + 1,298 + 1,008 + 0,695 + 0,616 + 0,664 + 0,853 + 0,985 + 0,997 = 12.

Получим следующие значения скорректированной сезонной компоненты (Таблица 4):

Таблица 4 - Значения скорректированной сезонной компоненты

Январь	S1	1,491	Июль	S7	0,695
Февраль	S2	0,987	Август	S8	0,616
Март	S3	1,250	Сентябрь	S9	0,664
Апрель	S4	1,155	Октябрь	S10	0,853
Май	S5	1,298	Ноябрь	S11	0,985
Июнь	S6	1,008	Декабрь	S12	0,997

Занесем полученные значения для соответствующих месяцев каждого года.

Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения скорректированной сезонной компоненты. Получим: T·E = Y / S, которые содержат только тенденцию и случайную компоненту.

Шаг 4. Определим компоненту T в мультипликативной модели. Для этого рассчитаем параметры линейного тренда, используя уровни (T·E). Результаты аналитического выравнивания:

Т = -64018,071 + 1201,064 · t; R ² = 0,863