Курсовая работа: Моделирование и прогнозирование естественного прироста населения в РФ
Таблица 8 - Статистика уравнения для модели с фиктивными переменными
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | |
| Y-пересечение | -89444,083 | 2879,238 | -31,065 | 2,76051E-20 |
| t | 1132,083 | 79,218 | 14,291 | 6,2844E-13 |
| D2 | 24047,583 | 3803,309 | 6,323 | 1,8825E-06 |
| D3 | 17218,167 | 3805,783 | 4,524 | 0,000152385 |
| D4 | 21431,750 | 3809,903 | 5,625 | 1,00291E-05 |
| D5 | 15077,333 | 3815,664 | 3,951 | 0,000634609 |
| D6 | 26904,583 | 3823,058 | 7,037 | 3,59459E-07 |
| D7 | 40734,833 | 3832,075 | 10,630 | 2,38467E-10 |
| D8 | 43809,083 | 3842,705 | 11,401 | 6,10242E-11 |
| D9 | 38606,667 | 3854,934 | 10,015 | 7,43321E-10 |
| D10 | 32848,917 | 3868,747 | 8,491 | 1,52119E-08 |
| D11 | 26662,833 | 3884,126 | 6,865 | 5,33422E-07 |
| D12 | 24437,083 | 3901,054 | 6,264 | 2,16207E-06 |
Проанализируем эти результаты. Все коэффициенты уравнения и само уравнение статистически значимы при уровне надежности 95%.
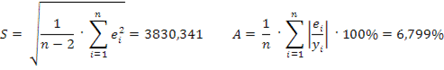
Исходя из значений выше приведенных показателей качества, можно сделать вывод о том, что модель обладает высокой точностью и пригодна для прогнозирования.
2.6 Адаптивная сезонная модель Тейла – Вейджа
Рассмотрим аддитивную модель сезонных явлений с линейным ростом, предложенную Г. Тейлом и С. Вейджем. Параметры адаптации определим методом последовательных итераций, исходя из принципа минимизации средней ошибки аппроксимации модели. В результате получим следующие значения: α1 = 0,9; α2 = 0,1; α3 = 0,1.
Тренд – линейный, уравнение тренда выглядит следующим образом:
T = -67660,089 + 1358,979 ·t; R 2 = 0,579
Начальные условия для нулевого цикла представлены в таблице 9:
Таблица 9 -Начальные условия
| i | ĝi0 | i | ĝi0 |
| 1 | -24733,642 | 7 | 14639,816 |
| 2 | -912,954 | 8 | 17487,170 |
| 3 | -7969,267 | 9 | 12057,857 |
| 4 | -3982,580 | 10 | 6073,211 |
| 5 | -10563,892 | 11 | -339,768 |
| 6 | 1036,462 | 12 | -2792,414 |
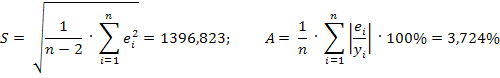
Исходя из значений выше приведенных показателей качества, можно сделать вывод о том, что модель обладает высокой точностью и пригодна для прогнозирования.
2.7 Прогнозирование естественного прироста населения
Рассмотрим прогнозные значения естественного прироста населения в РФ по вышеописанным моделям, сравним полученные значения с фактическими, и выберем наиболее адекватную и точную модель для целей прогнозирования (Таблица 10).
Для оценки точности каждого прогноза рассчитаем среднюю относительную ошибку прогноза по формуле:
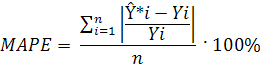
Таблица 10 - Прогнозные значения
| Адд. модель | Мультипл. модель | Ряд Фурье | Модель с фикт. переменными | Адапт. модель Тейла-Вейджа | Фактические значения | |
| Январь 2009 | -41595 | -29184 | -38887 | -47557 | -46805 | -47976 |
| Февраль 2009 | -19866 | -18134 | -31056 | -22377 | -22944 | -24401 |
| Март 2009 | -29093 | -21475 | -21699 | -28075 | -29994 | -32121 |
| Апрель 2009 | -24284 | -18459 | -23375 | -22729 | -26006 | -27017 |
| Май 2009 | -27749 | -19177 | -24958 | -27951 | -32588 | -28463 |
| Июнь 2009 | -15685 | -13678 | -13849 | -14992 | -20989 | -19821 |
| Июль 2009 | -304 | -8598 | -86 | -30 | -7384 | -4237 |
| Август 2009 | 3999 | -6886 | 2590 | 4177 | -4539 | 1050 |
| Сентябрь 2009 | 2212 | -6624 | -348 | 106 | -9968 | -3263 |
| Октябрь 2009 | -5701 | -7484 | -426 | -4519 | -15951 | -12170 |
| Ноябрь 2009 | -9688 | -7452 | -4684 | -9573 | -22368 | -25891 |
| Декабрь 2009 | -9265 | -6350 | -17547 | -10667 | -24818 | -25116 |
| Средняя относит. ошибка прогноза (%) | 66,260 | 111,627 | 56,422 | 62,296 | 74,758 | - |
Исходя из показателя средней относительной ошибки прогноза, можно сделать вывод о том, что показатель естественного прироста населения наиболее точно прогнозируется рядом Фурье.
Заключение
В ходе работы было проведено моделирование и прогнозирование естественного прироста населения в РФ. Исследование было проведено с помощью следующих моделей:
· Аддитивная модель;
· Мультипликативная модель;
· Одномерный анализ Фурье;
· Регрессионная модель с переменной структурой (фиктивные переменные);
· Адаптивная сезонная модель.
Выдвинутая гипотеза о возрастающей тенденции динамики изменения естественного прироста населения в РФ в 2009 году подтверждается.
По каждой модели сделан прогноз на 2009 год, при этом следует отметить, что наиболее точный прогноз дает модель с использованием ряда Фурье, в тоже время вариацию исходного показателя наиболее точно описывает адаптивная модель Тейла – Вейджа. Также можно сделать вывод о том, что для получения наиболее достоверного прогноза показателя необходимо комбинировать прогнозные значения нескольких наиболее точных моделей.
Список литературы
1. StatSoft // http://www.statsoft.ru/
2. Агентство АКДИ // http://www.akdi.ru/
3. Концепция демографической политики Российской Федерации на период до 2015 года // http://www.akdi.ru/econom/program/demogr.htm