Курсовая работа: Моделирование и прогнозирование естественного прироста населения в РФ
Уравнение описывает на 86,3% вариацию исходного показателя естественного прироста, при этом уравнение является статистически значимым при уровне надежности 95%.
Подставляя в это уравнение значения t = 1,…,36, найдем уровни Т для каждого момента времени.
Шаг 5. Найдем уровни ряда по мультипликативной модели, умножив уровни Т на значения скорректированной сезонной компоненты для соответствующих месяцев.
Шаг 6. Расчет ошибки в мультипликативной модели производится по формуле:
E = Y / (T·S)
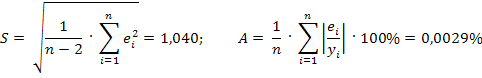
Исходя из значений выше приведенных показателей качества, можно сделать вывод о том, что модель обладает высокой точностью и пригодна для прогнозирования.
2.4 Одномерный анализ Фурье
Выполним одномерный анализ Фурье для показателя естественного прироста населения РФ. Расчетная таблица ряда Фурье представлена в Приложении 5.
Переменными для составления модели будут следующие: t, cos(2·Π·t/12); sin(2·Π·t/12); cos(4·Π·t/12); sin(4·Π·t/12); cos(6·Π·t/12); sin(6·Π·t/12).
Значение знаменателя каждой дроби обусловлено периодичностью сезонных колебаний.
Построив модель с включением данных переменных, получаем следующее уравнение:
Ŷt = -64314,412 + 1178,132 · t – 5360,004 ·cos(2·Π·t/12) –12253,175 ·sin(2·Π·t/12) – 4098,437 ·cos(4·Π·t/12) + 1894,178 ·sin(4·Π·t/12) + 933,424 ·cos(6·Π·t/12) –5109,257 ·sin(6·Π·t/12); R 2 = 0,897
Таблица 6 - Статистика уравнения для модели ряда Фурье
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | |
| Y-пересечение | -64314,412 | 2390,342 | -26,906 | 1,49932E-21 |
| t | 1178,132 | 113,994 | 10,335 | 4,62652E-11 |
| cos(2Pi*t/12) | -5360,004 | 1595,524 | -3,359 | 0,002267582 |
| sin(2Pi*t/12) | -12253,175 | 1647,329 | -7,438 | 4,22248E-08 |
| cos(4Pi*t/12) | -4098,437 | 1595,524 | -2,569 | 0,015828755 |
| sin(4Pi*t/12) | 1894,178 | 1603,648 | 1,181 | 0,247471866 |
| cos(6Pi*t/12) | 933,424 | 1595,524 | 0,585 | 0,56321529 |
| sin(6Pi*t/12) | -5109,257 | 1595,524 | -3,202 | 0,003385848 |
Уравнение описывает на 89,7% вариацию исходного показателя естественного прироста, при этом уравнение является статистически значимым при уровне надежности 95%.
Но коэффициенты перед переменными sin(4·Π·t/12) и cos(6·Π·t/12) не удовлетворяют данному уровню надежности.
Исключим их из модели и перестроим уравнение регрессии.
Ŷt = -64096,083 + 1166,330 · t –5348,202 · cos(2·Π·t/12) –12297,219 · sin(2·Π·t/12) –4086,636 · cos(4·Π·t/12) – 5121,059 · sin(6·Π·t/12); R2 = 0,891
Таблица 7 - Статистика уравнения для модели ряда Фурье
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | |
| Y-пересечение | -64096,083 | 2361,646 | -27,140 | 1,138E-22 |
| t | 1166,330 | 112,370 | 10,379 | 1,90859E-11 |
| cos(2Pi*t/12) | -5348,202 | 1588,773 | -3,366 | 0,002101931 |
| sin(2Pi*t/12) | -12297,219 | 1639,342 | -7,501 | 2,31486E-08 |
| cos(4Pi*t/12) | -4086,636 | 1588,773 | -2,572 | 0,015299504 |
| sin(6Pi*t/12) | -5121,059 | 1588,773 | -3,223 | 0,003049779 |
Уравнение описывает на 89,1% вариацию исходного показателя естественного прироста, уравнение статистически значимо при уровне надежности 95%. Все коэффициенты уравнения статистически значимы при аналогичном уровне надежности.
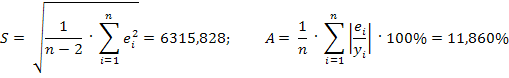
Модель имеет высокие показатели среднеквадратической ошибки и средней ошибки аппроксимации, но может быть использована для прогнозирования.
2.5 Регрессионная модель с переменной структурой (фиктивные переменные)
Рассмотрим еще один метод моделирования временного ряда, содержащего сезонные колебания, - построение модели регрессии с включением фактора времени и фиктивных переменных. Количество фиктивных переменных в такой модели должно быть на единицу меньше числа моментов (периодов) времени внутри одного цикла колебаний. В данном случае при моделировании ежемесячных данных модель должна включать двенадцать независимых переменных – фактор времени и одиннадцать фиктивных переменных. Каждая фиктивная переменная отражает сезонную (циклическую) компоненту временного ряда для какого-либо одного периода. Она равна единице для данного периода и нулю для всех остальных периодов.
Построим модель регрессии с включением фактора времени и фиктивных переменных для данных о естественном приросте населения в РФ. В данной модели двенадцать независимых переменных: t, D2, D3, D4, D5, D6, D7, D8, D9, D10, D11, D12 и результативная переменная Y. Составим матрицу исходных данных (Приложение 6).
Уравнение регрессии имеет вид:
Ŷt = -89444,083 + 1132,083 · t + 24047,583 ·D2 + 17218,167 ·D3 + 21431,750 ·D4 + 15077,333 ·D5 + 26904,583 ·D6 + 40734,833 ·D7 + 43809,083 ·D8 + 38606,667 ·D9 + 32848,917 ·D10 + 26662,833 ·D11 + 24437,083 ·D12
R 2 = 0,960
Уравнение описывает на 96,0% вариацию исходного показателя естественного прироста, уравнение статистически значимо при уровне надежности 95%.