Здесь условие 2) гарантирует регулярность марковского процесса, который не может за конечное время делать бесконечное число скачков из одного состояния в другое.

Замечание 2.2 . Если условие (2.1.24) выполнено во всех узлах и ряд (2.1.25) сходится, то получается простой алгоритм для нахождения стационарных вероятностей:

1. Решается система линейных уравнений (2.1.1).

2. Проверяется выполнение условия (2.1.24).

3. Определяется по формуле (2.1.26) и проверяется сходимость ряда (2.1.25).

4. Определяются с помощью соотношения

где

(Формулы (2.1.28), (2.1.29) получаются из (2.1.18), (2.1.19) с учетом персонификации -го узла и того, что на него в изоляции направляется простейший поток с параметром ).

5. Находится стационарное распределение состояний сети с помощью формулы (2.1.2).

При этом нормировку вероятностей можно производить не раз, как это делалось в пункте 4, а один раз, исходя из условия . Отметим также, что если в сети есть терминальные узлы, в которых условие (2.1.24) не выполняется, то алгоритм существенно усложнится, так как в этих узлах нельзя применить (2.1.28), (2.1.29). Поэтому для таких узлов необходимо добавить процедуру численного решения системы уравнений (2.1.3) – (2.1.8) с последующей его нормировкой.

Замечание 2.3 . Нетрудно понять, что совместное стационарное распределение чисел заявок в узлах имеет следующую форму:

где

а совместное стационарное распределение режимов работы узлов – форму:

где

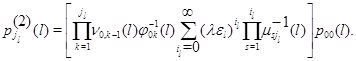
Исходя из этих соотношений можно построить также алгоритм подсчета числовых характеристик узлов в стационарном режиме. Например, можно найти среднее стационарное число заявок в каждом узле, средний стационарный режим работы каждого узла и т.п. В принципе можно построить алгоритм нахождения совместной стационарной производящей функции чисел заявок и режимов работы в узлах сети, алгоритмы нахождения совместной производящей функции чисел заявок и нахождения совместной производящей функции режимов работы узлов в установившемся состоянии.

Пусть – часть выходящего из -го узла потока заявок, покидающих сеть – подмножество нетерминальных узлов . Из леммы 2.2 и результатов работы вытекает

Следствие 1.1 [43, C.133] . Потоки являются независимыми пуассоновскими потоками с параметрами соответственно .

Заметим, что если условию (2.1.23) подчиняются все узлы, то – независимые пуассоновские потоки.

2 Сети с переключением режимов при определенном количестве заявок в узле

Пусть , где – вектор, все координаты которого равны нулю кроме – вектор, все координаты которого равны нулю кроме . На фазовом пространстве задан многомерный марковский процесс , где , своими инфинитезимальными интенсивностями перехода

Интенсивности перехода из состояния во все состояния, отличные от вышеперечисленных, предполагаются равными нулю. Здесь , если и , если и и .