Курсовая работа: Одноосьовий гіроскопічний стабілізатор

3) Побудуємо на комплексній площині (Х0У) криву Найквіста та зробимо висновок про стійкість системи:

У(ω) = 0 → ω = 0 → Х(0) = 0;

У(ω) = 0 → ω = =12,909 →

Х(12,909) = = -0,141.

По цим точкам побудуємо криву Найквіста (рис. 5).

Критерій Найквіста: Для того щоб замкнута система була стійкою необхідно, щоб годограф розімкненої системи починаючись на дійсній вісі і рухаючись проти годинникової стрілки (при змінній частоті від 0 до ∞) не охоплював точку (-1, j0).

Рис. 5. Крива Найквіста

Замкнена САК не охоплює точку (-1, j0), що видно на рис. 5. Отже, САК стійка.

б). Дослідження системи методом D – розбиття

За даними, що були отримані в пункті 3.3 знайдемо критичний коефіцієнт підсилення системи kкр:

0,32 ≥ k·0,006

k ≤ 53

k = 53 (теоретично розрахований коефіцієнт підсилення).

Використовуючи методику D-розбиття та за допомогою програми MathCad побудуємо межу D-розбиття, обравши за параметр дослідження коефіцієнт підсилення системи.

Характеристичний поліном САК, враховуючи, що параметр, який досліджується, коефіцієнт підсилення:

D(p) = .

Звідси k(p) = і k(ωj) =

Побудуємо область D-розбиття, знаючи, що Re(k) = , Im(k) = = (див. рис. 6).

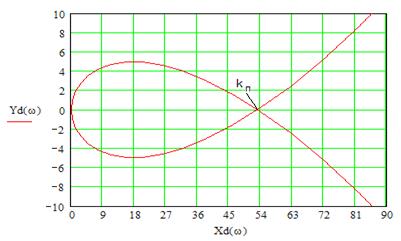
Рис. 6. Область стійкості за параметром k

На побудованій області D- розбиття можна визначити коефіцієнт підсилення (точка перетину області з дійсною віссю).

3.5 Побудова логарифмічної частотної характеристики САК та визначення

запасів стійкості

1) Знаючи перехідну характеристику розімкненої САК

w(s)=,

знайдемо нульову контрольну точку: L0 = 20lgk = 20lg7,5 = 17,5 дБ.

2) Визначимо спряжені частоти: ω1 = = 50с-1; ω2 = = 3,3с-1.

3) Враховуючи, що до складу системи входить пропорційна, інтегруюча та дві аперіодичні ланки першого порядку ЛАХ і ЛФХ для даної САК (рис. 7).

Рис. 7. Відповідно логарифмічно амплітудна та логарифмічно частотна характеристики системи автоматичного керування

Як видно з графіків, оскільки ЛАХ перетинає вісь 0ω під нахилом -40, а ЛФХ перетинає пряму –π, система є нестійкою.

Знайдемо запаси стійкості системи за ЛАХ та ЛФХ:

· по амплітуді: ΔL = 20lg (w(j*ωс)), де ωс – частота, за якої φ(ωc) = -π. З графіка видна ωc = 6 (див. рис.7). Тоді

ΔL = 20lg (w(j*ωс)) = 20lg (w(j*6)) = -17.

Порівнюємо з значенням визначеним критерієм Найквіста h=20lg(|1/Wcp|) = =20lg(|1/6|)= 17,016 з h=17 знайденому по рис. 7.