Курсовая работа: Одноосьовий гіроскопічний стабілізатор

- помилка від вхідної керуючої дії.

- усталена похибка.

Рис. 11. Графік похибки САК

- при сигналі G2(t) = 100t (рис. 12),

- помилка від вхідної керуючої дії.

- усталена похибка.

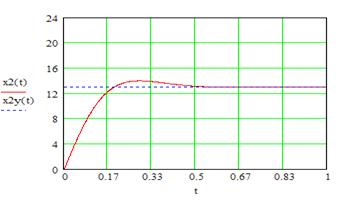
Рис. 12. Графік усталеної похибки САК

3.10 Оцінка якості скорегованої САК

Оцінимо якість перехідних процесів у заданій системі:

- перерегулювання δ – відносне максимальне відхилення перехідної характеристики від усталеного значення вихідної координати, виражене у відсотках:

δ =

(hmax, hуст – відповідно максимальне та усталене значення перехідної характеристики для досліджуваної системи побачимо на графіку (рис.10))

δ = .

- час регулювання (час перехідного процесу) tp – мінімальний час, після сплину якого регульована координата буде залишатися близькою до усталеного значення із заданою точністю .

, тоді tp = 0,6 (с).

- число коливань n, яке має перехідна характеристика h(t) за час регулювання tp:

n = 1.

Висновок: приведені вище розрахунки та дослідження показують, що задана система є нестійкою, але її можна скорегувати порівняно нескладними корегуючими пристроями (передаточна функція після корегування має пропорційну, інтегруючу та дві аперіодичні ланки першого порядку), метод розрахунку яких приведений вище; при роботі системи спостерігали усталену похибку САК з заданою вхідною дією, розрахунок провели за допомогою приведених вище формул.

3.11 Моделювання системи в програмному модулі Simulink

Змоделюємо систему в програмному модулі Simulink – зберемо структурну схему отриманої скоректованої системи (рис. 13).

Рис. 13. Модель скоректованої САК в програмному модулі Simulink

1) Реакція системи на одиничний ступінчатий сигнал (рис. 14).

Рис. 14. Реакція системи на одиничний вхідний сигнал

Порівнюючи реакцію САК, отриману за допомогою моделювання (рис. 14), з теоретично отриманою перехідною характеристикою (рис. 10) в пункті 3.8 виявили, що вони співпали (розрахунки в обох випадках проведені правильно).

2) Побудова графіка вихідної координати при заданій вхідній дії

g(t) = 100t (рис. 16).

Змоделюємо систему з заданою вхідною дією в програмному модулі Simulink (рис. 15).

Рис. 15. Модель САК з заданою вхідною дією

Реакція системи на вхідний сигнал (рис. 16).

Рис. 16. Реакція САК на задану вхідну дію

З графіків видно, що робота системи залежить від вхідного сигналу.

4 Аналіз дискретної САК (ДСАК)

В основі аналізу дискретної САК візьмемо лінійну неперервну САК після корекції з передаточною характеристикою w(s) = .

4.1 Визначення періоду дискретизації імпульсного елемента.

В якості формоутворювача сигналу приймемо екстраполятор нульового порядку.

ωз = 43,2 с-1 – максимальна частота в спектрі вхідного сигналу.

За теоремою Котельникова для нормальної роботи системи необхідно, щоб виконувалася умова Tk = - період дискретизації, ωк ≥ 2ωз – частота дискретизації. Оберемо ωк ≥ 2·43,2 = 86,4 с-1, тоді

Tk ≤ (с)

Виберемо період дискретизації Tk = 0,01с, ωк = 90 с-1.

4.2 Визначення передаточної функції розімкнутої та замкнутої ДСАК відносно вхідної дії