Курсовая работа: Основы практического использования прикладного регрессионного анализа
![]() - вектор возмущений размерностью
- вектор возмущений размерностью ![]() ;
;
![]() - количество независимых переменных;
- количество независимых переменных;
![]() - количество экспериментальных данных;
- количество экспериментальных данных;
![]() - класс функциональных зависимостей.
- класс функциональных зависимостей.
В зависимости![]()
![]()
![]() – является случайной величиной, значения
– является случайной величиной, значения ![]() могут рассматриваться либо как фиксированные, либо как случайные. При этом ожидаемое значение одной случайной переменной соотносится с наблюдаемыми значениями других случайных переменных в виде условной регрессии.
могут рассматриваться либо как фиксированные, либо как случайные. При этом ожидаемое значение одной случайной переменной соотносится с наблюдаемыми значениями других случайных переменных в виде условной регрессии.
Рассмотрим зависимость между случайными величинами ![]() и
и ![]() , представленную в виде некоторой таблицы наблюдений значений
, представленную в виде некоторой таблицы наблюдений значений ![]() и
и ![]() .
.
Перенося табличные значения ![]() и
и ![]() на плоскость
на плоскость ![]() , получаем поле корреляции, приведенное на рисунке 3.1
, получаем поле корреляции, приведенное на рисунке 3.1

Рисунок 1.1 — Экспериментальное уравнение регрессии
Разобьем диапазон изменения ![]() на
на ![]() -равных интервалах
-равных интервалах ![]() . Все точки, попавшие в интервал
. Все точки, попавшие в интервал ![]() , отнесем к середине интервала
, отнесем к середине интервала ![]() , в результате получаем трансформированное поле корреляции.
, в результате получаем трансформированное поле корреляции.
Определим частичные средние арифметические ![]() для каждого значения
для каждого значения ![]() :
:
![]() ,
,
где ![]() - число точек, оказавшихся в интервале
- число точек, оказавшихся в интервале![]() , причем
, причем ![]() , где
, где
![]() - общее число наблюдений.
- общее число наблюдений.
Соединим последовательно точки с координатами ![]() и
и ![]() отрезками прямых. Полученная ломаная линия называется эмпирической линией регрессии
отрезками прямых. Полученная ломаная линия называется эмпирической линией регрессии ![]() по
по ![]() ; она показывает, как в среднем меняется
; она показывает, как в среднем меняется ![]() с изменением
с изменением ![]() . Предельное положение эмпирической линии регрессии, к которому она стремится при неограниченном увеличении числа наблюдений и одновременном уменьшении
. Предельное положение эмпирической линии регрессии, к которому она стремится при неограниченном увеличении числа наблюдений и одновременном уменьшении ![]() , называется предельной теоретической линией регрессии. Ее нахождение и составляет основную задачу регрессионного анализа. Отметим, что по линии регрессии невозможно точно определить значение
, называется предельной теоретической линией регрессии. Ее нахождение и составляет основную задачу регрессионного анализа. Отметим, что по линии регрессии невозможно точно определить значение ![]() по
по ![]() в одном опыте. Однако зависимость
в одном опыте. Однако зависимость ![]() позволяет определить в среднем значение
позволяет определить в среднем значение ![]() при многократном повторении опыта при фиксированном значении
при многократном повторении опыта при фиксированном значении ![]() . В регрессионном анализе рассматривается связь между одной переменной, называемой зависимой, и несколькими другими, называемыми независимыми. Эта связь представляется в виде математической модели, т.е. в виде функции регрессии. Если функция линейна относительно параметров, но не обязательно линейна относительно независимых переменных, то говорят о линейной модели. В противном случае нелинейная. Статистическими проблемами обработки в регрессионном анализе являются:
. В регрессионном анализе рассматривается связь между одной переменной, называемой зависимой, и несколькими другими, называемыми независимыми. Эта связь представляется в виде математической модели, т.е. в виде функции регрессии. Если функция линейна относительно параметров, но не обязательно линейна относительно независимых переменных, то говорят о линейной модели. В противном случае нелинейная. Статистическими проблемами обработки в регрессионном анализе являются:
а) Получение наилучших точечных и интервальных оценок неизвестных параметров регрессионного анализа;
б) Проверка гипотез относительно этих параметров;
в) Проверка адекватности;
г) Проверка множества предполагаемых предположений.
Исследуемый объект представлен на рисунке 3.2
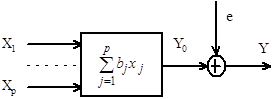
Рисунок 1.2 — Вид исследуемого объекта
Для корректного использования регрессионного анализа существует следующие предпосылки и следующие допущения на свойства регрессионной ошибки ![]() ,
, ![]() ;
; ![]() - значение зависимой переменной, полученное подстановкой
- значение зависимой переменной, полученное подстановкой ![]() в уравнение
в уравнение ![]() ,
, ![]() ,
, ![]() ;
; ![]() - количество экспериментальных данных,
- количество экспериментальных данных, ![]() - количество независимых переменных:
- количество независимых переменных:
Приведем свойства и предпосылки регрессионной ошибки:
а) Свойства регрессионной ошибки:
1) В каждом опыте ![]() имеет нормальный закон распределения;
имеет нормальный закон распределения;
![]() ,
, ![]() .
.
2) В каждом опыте математическое ожидание ![]() равно нулю;
равно нулю;
![]() ,
, ![]() .
.