Курсовая работа: Основы практического использования прикладного регрессионного анализа

.

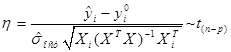Задавшись уровнем значимости и найдя табличное значение можно построить достоверный интервал для в виде

.

1.4.4 Свойства доверительных интервалов

а) Доверительный интервал симметричен относительно выборочной оценки ;

б) Ширина доверительного интервала зависит от и ;

в) Ширина доверительного интервала минимальна, если , (ортогональны);

г) Ширина доверительного интервала равна бесконечности, если:

вектор-столбцы и в матрице наблюдений коллинеарные, т.е.если:

д) В общем случае в регрессионных уравнениях доверительный интервал для отдельно взятого регрессионного коэффициента определяется выражением

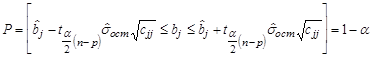
1.5 Адекватность модели

Существует соотношение, которое можно использовать для оценки адекватности модели, сравнивая и . Расчетное определяется по формуле

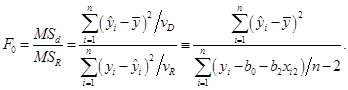(3.4)

Табличное значение берется с таблиц с определенным числом степенем свобода и для притятого уровня значимості .Если расчетное значение більше , то это значит, что дисперсияMSR статистически меньше дисперсии MSD относительно ,в этом случае полученное уравнение регрессии можно считать дееспособным.

2. ПРАКТИЧЕСКАЯ ЧАСТЬ

Поставлена следующая задача: построить зависимость количества выигранных голов от характеристик сыгранных игр на основе модели множественной регрессии.

На основе имеющейся выборки сделаем следующие оценки:

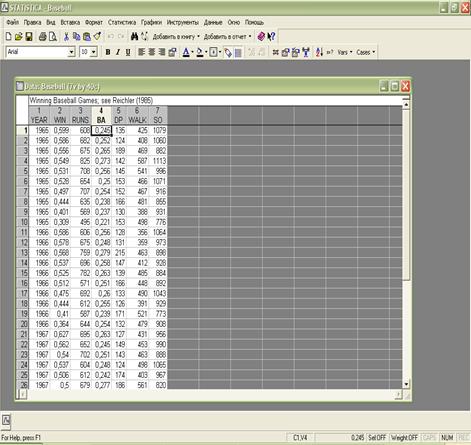
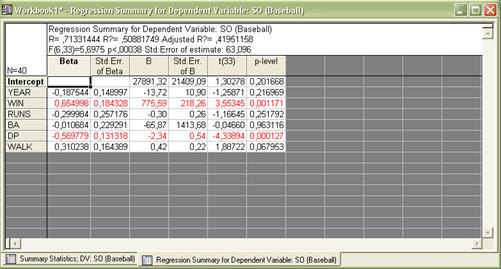
1) параметры модели β_i (для данной модели существенными являются переменные WIN и DP):

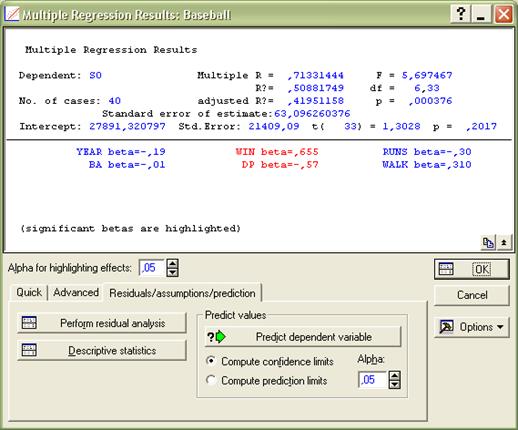
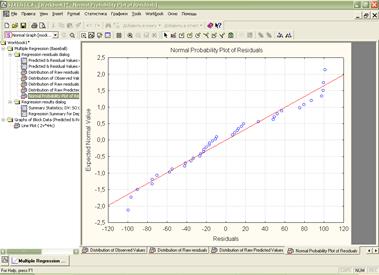
2) оценки: множественный коэффициент корреляции R, R² ,F, p, и StdErrorofestimate:

3) график для вычисленных значений и исходных:

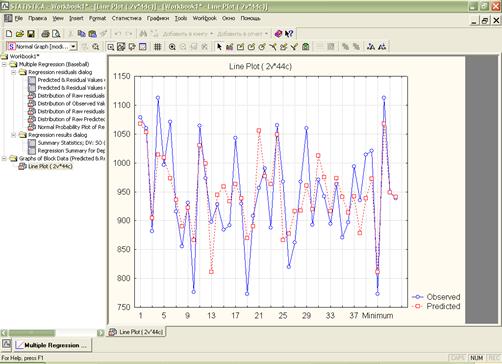
К такому ряду можно применить модель линейной регрессии, так как он стационарный;

4) построение регрессии: