Курсовая работа: Параллельный перенос в пространстве Лобачевского

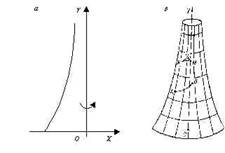
Рисунок 2

Двумерный аналог геометрии Лобачевского: трасоида (а) и псевдосфера, образованная вращением трасоиды вокруг оси ОY (б ).

АВ – геодезическая (кратчайшее расстояние между точками А и В в пространстве Лобачевского. KLM – треугольник в пространстве Лобачевского; Ð + Ð L + Ð М < 180°.

Наглядный образ, соответствующий трехмерной геометрии Лобачевского, построить не удается, так как геометрия в обыденном представлении остается евклидовой. Однако удалось доказать логическую непротиворечивость и существование такой геометрии. Основная идея доказательства заключается в том, чтобы свести геометрию Лобачевского, построенную как планиметрию (т.е. на плоскости), к геометрии на трехмерной гиперповерхности постоянной отрицательной кривизны (аналогом такой гиперповерхности-псевдосферы может быть трехмерный гиперболоид) в четырехмерной евклидовой геометрии. Модель трехмерной геометрии Лобачевского можно представить в виде бесконечной седловидной поверхности гиперболической формы, поэтому такую геометрию обычно называют гиперболической.

Риман обобщил геометрические представления и создал теорию произвольно искривленных пространств. Заслуга его состоит и в разработке частных случаев неевклидовых геометрий, в том числе в создании эллиптической геометрии, выступающей антитезой гиперболической геометрии Лобачевского. Эллиптическая геометрия – это геометрия на трехмерной гиперсфере. Двумерной ее аналогией является геометрия на поверхности обычной сферы. Здесь можно видеть, что представление о параллельных линиях вообще теряет всякий смысл, ибо все “параллельные” в локальном смысле линии представляют собой линии большого круга, пересекающиеся на полюсах сферы, а сумма углов треугольника, образованных этими линиями, всегда больше 180°.

Следует особо отметить, что при малых величинах неевклидовы геометрии можно считать евклидовыми.

Вот три рода изменений кривизны в пространстве, которые мы должны признать лежащими в пределах возможного:

I. Пространство наше, быть может, действительно обладает кривизной, меняющейся при переходе от одной точки к другой, – кривизной, которую нам не удается определить или потому, что мы знакомы лишь с небольшой частью пространства, или потому, что смешиваем незначительные происходящие в нем изменения с переменами в условиях нашего физического существования, последние же мы не связываем с переменами в нашем положения...

II. Наше пространство может быть действительно тождественно во всех своих частях (имеет одинаковую кривизну), но величина его кривизны может изменяться как целое во времени. В таком случае наша геометрия, основанная на тождественности пространства, сохранит свою силу для всех частей пространства, по перемены в кривизне могут произнести в пространстве ряд последовательных видимых изменений.

III. Мы можем мыслить наше пространство как имеющее повсюду приблизительно однородную кривизну, но легкие изменения кривизны могут существовать при переходе от одной точки к другой, в свою очередь изменяясь во времени. Эти изменения кривизны во времени могут произвести явления, которые мы не так уж неестественно приписываем физическим причинам, не зависящим от геометрии нашего пространства”

Интересно то, что все эти три варианта изменения кривизны пространства нашли свое воплощение в общей теории относительности.

2 ОПИСАНИЕ ПРОСТРАНСТВА ЛОБАЧЕВСКОГО

Представим отрезок АB в прямоугольной системе координат (евклидово пространство). Его длина определится по теореме Пифагора как

(AВ )² = (x ₂ - x ₁ )² + (у ₂ - у ₁ )² , (1) ??? x ₁ , x ₂ , y ₁ , y ₂ ? ???????? ?????? ??????? АВ ?? ??? Х ? Y, ???
(AB)² = Dx^{2 +} Dy² . (2)

Для бесконечно малого расстояния между двумя точками принят символ ds. Поэтому, если точки А и В сближаются все больше и больше, можно написать

ds² = dx^{2 +} dy² (3)

Предположим, что система координат относительно начала координат О повернулась на некоторый угол α.

Обозначим новую систему координат как X'Y'. Тогда расстояние между точками, не изменившееся по величине, запишем как

ds ² = dx' ² + dy' ² . (4)

Поскольку при любом вращении или параллельном переносе координат величина расстояния не изменяется, она называется инвариантной относительно преобразования координат.Для косоугольной системы координат квадрат длины отрезка АВ, который называется в общем и строгом смысле квадратом интервала, запишем (на основе той же теоремы Пифагора) в виде

ds ² = dx ² + dy ² + 2 dxdy cos α(5)

При этом, как можно видеть, численное значение интервала не изменяется, хотя формула для его выражения имеет более сложный вид, чем формула (3), т.е. и в данном случае интервал является инвариантом относительно замены координат.

Рассмотрим описание интервала в неевклидовой геометрии. Но чтобы лучше понять смысл этого описания, сравним геометрию двумерного пространства с геометрией двумерной сферы. В качественном отношении эти пространства одинаково однородны и изотропны, так как и в случае сферы все ее точки эквивалентны относительно поворотов осей координат или их параллельного переноса.

Введем сферическую систему координат. Она состоит из заданной фиксированной точки О, из произвольно ориентированной в пространстве прямой ρ, проходящей через центр О, из полуплоскостей, ограниченных этой прямой, из конических поверхностей с вершиной в точке О и прямой ρ в качестве оси и из сфер с центром в точке О. Прямая ρ как радиус есть параметр семейства сфер с центром О. Параметром семейства полуплоскостей является угол φ, который образует полуплоскость с так называемой полуплоскостью нулевого меридиана (аналогична географической долготе). Параметр семейства конических поверхностей – угол раствора θ, который измеряется между положительным направлением прямой ρ и образующей боковой поверхности конуса (полярный угол).

Выберем из семейства сфер, задаваемых параметром ρ, некоторую сферу радиусом r ( ρ = r). Тогда координаты точки А на поверхности сферы определяются на основе сказанного следующим образом. Зафиксируем большой круг QQ', называемый экватором, и большой круг PР', называемый пулевым меридианом (Р и Р' – полюса). Большие полукруги сферы, исходящие из полюса Р, называются меридианами, малые круги, параллельные экватору, – долготами. Угол φ, т.е. угол между нулевым меридианом и меридианом точки A (азимутальный угол), отсчитываемый против часовой стрелки (долгота), и угол θ, отсчитываемый от полюса Р до долготы точки А (полярный угол), вполне задают координаты точки А. Аналогичным образом определяются координаты точки В. Тогда интервал между двумя бесконечно близкими точками А и В (элементарный интервал АВ) можно получить из выражения

ds² = r ² sin² qd j² + r ² d q² . (6)

Выражение (6) никакими преобразованиями нельзя свести к простой формуле (3) одновременно для всей поверхности сферы. Такую операцию можно осуществить лишь локально, выбирая направление на бесконечно малом участке сферы, так чтобы Ðq = 90°, и это фиксирует систему координат применительно только к данному участку сферы. В целом же, глобально, сделать это невозможно, что отражает неевклидовость сферы.

Следующий шаг по пути обобщения представления пространственного интервала связан с его описанием на любой произвольной криволинейной поверхности. Из анализа сферической системы координат мы видим, что вводятся элементы, фиксирующие тот факт, что поверхность искривлена, т.е. углы и радиус, которые, однако, при минимальной значимой локализации (грубо говоря, “выпрямлении” кривизны, представлении каждой достаточно малой локальной области поверхности в виде плоскости) дают инвариантный интервал – интервал, не изменяющий своей величины при преобразовании координат.

Представим, что мы имеем координатные линии любого искривления, в наиболее простом виде – косоугольные (гауссовы) с двумя измерениями U и V. Тогда

ds² = К du² + 2L du dv + М dv² , (7)

где К, L, М – величины, меняющиеся от точки к точке, т.е. характеризующие искривление поверхности. Эти величины могут измеряться с помощью бесконечно малых масштабов длины и угла и характеризуют геометрию самой поверхности.

Прикладывая бесконечно малые интервалы друг к другу, мы можем найти кратчайшее расстояние между двумя точками, которое в самом общем случае называется геодезической. Последняя является аналогом прямой линии в декартовой прямоугольной системе координат (евклидовом пространстве). Для каждого бесконечно малого интервала мы можем построить окружности и на этой основе определить соответствующие углы (предлагаем сравнить со сферической системой координат). Прямые линии и углы позволяют нам проводить любые геометрические построения.

Эти линии и углы с геометрической (но не с физической) точки зрения поддаются точным измерениям. Если поверхность евклидова декартовой системой координат, то наши измерения подтвердят аксиомы Евклида. Если поверхность – сфера, то постулат о параллельности прямых не выполняется. Не выполняется и постулат о бесконечной протяженности прямой линии. В этом случае каждая прямая, лежащая в одной плоскости с данной прямой, пересекает ее, а движение от данной точки по прямой снова приведет в эту данную точку независимо от направления перемещения. Если же поверхность образована вращением трасоиды вокруг оси (простейшая псевдосфера Лобачевского), то через точку, лежащую вне данной прямой, проходит более чем одна линия, лежащая в одной плоскости с данной прямой и не пересекающая ее.

Можно сказать, что кривизна – это величина, характеризующая отклонение кривой (линии либо поверхности) от прямой (линии или плоскости). Отклонение дуги АА' кривой L от касательной АВ к точке А можно описать так называемой средней кривизной k_cp этой дуги, равной отношению величины угла α между касательными в точках А и А' к длине s дуги АА':

(8)