Курсовая работа: Перетворення Фур’є. Спектри неперіодичних функцій

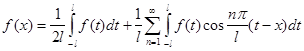(2.3)

Дістанемо граничну форму цього розвинення при . Оскільки функція абсолютна інтегрована на всій числовій осі, то при граничному переході при перший доданок у правій частині (2.3) прямує до нуля

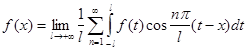(2.4)

Позначимо та перепишемо (2.4) як

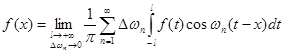(2.5)

При інтеграл 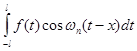можна замінити інтегралом

, а суму

можна вважати за інтегральну суму для інтеграла

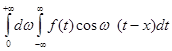
Таким чином, з рівності (2.5) дістаємо

(2.6)

Рівність (2.6) називається інтегральною формулою Фур’є, а інтеграл у її правій частині - інтегралом Фур’є. Зображення функції у вигляді інтеграла Фур’є звичайно називають розкладанням цієї функції в інтеграл Фур’є.

Зауваження 1. Формула (2.6) має сенс тільки для точок неперервності функції , а у кожній точці розриву першого роду, як і для рядів Фур’ є, інтеграл Фур’є збігається до числа

.

Формулу (2.6) приводимо до вигляду, що є збіжним з рядом Фур’ є:

(2.7) де

(2.8)

Рівність (2.7) аналогічна розвиненню функції в тригонометричний ряд Фур’є, а вираз (2.8) - формулам для коефіцієнтів Фур’ є. І, таким чином, (2.7) можна трактувати як розкладання неперіодичної функції, визначеної на всій числовій осі на суму гармонічних складових частоти , які неперервно заповнюють дійсну піввісь

Зауваження 2. Якщо функція - парна, то та інтеграл Фур’є для такої функції має вигляд

(2.9)

У випадку непарної функції

інтеграл Фур’є набуває вигляду

(2.10)

Приклад 1. Зобразити інтегралом Фур’є неперіодичну функцію

Дана функція задовольняє умовам зображення її інтегралом Фур’є. За формулами (2.8) і (2.7)