Курсовая работа: Перетворення Фур’є. Спектри неперіодичних функцій

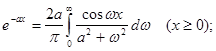
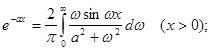
3. Спектральна характеристика (щільність) неперіодичної функції

У відповідності з формулою (2.22), неперіодична функція зображується сукупністю нескінченно великої кількості гармонік з нескінченно малими амплітудами у всьому діапазоні частот до . Функцію , визначену для неперіодичної функції за формулою (2.19) чи (2.22), називають спектральною характеристикою (спектральною щільністю, спектральною функцією) функції . ЇЇ модуль і аргумент називають відповідно амплітудною та фазовою спектральними характеристиками (відповідно амплітудно-частотним та фазочастотним спектрами).

Деякі властивості спектральної характеристики. Нехай - спектральна характеристика (це символічно можна записати . Тоді спектральній характеристиці (у випадку двобічного перетворення Фур'є) притаманні такі властивості [3]:

Лінійність де ;

Диференціювання оригіналу , якщо абсолютно інтегрована функція. Інтегрування оригіналу за умови, що . Диференціювання спектральної функції у випадку, коли - абсолютно інтегрована функція

Зміна масштабу незалежної змінної .

Зсув незалежної змінної .

Зсув спектральної функції

Множення функції на косинус та синус

Функція - комплексно - спряжена для функції , і, оскільки модулі спряжених функцій і рівні, а аргументи - відрізняються знаком, то амплітудно-частотний спектр - завжди парна, а фазо-частотний спектр - завжди непарна функція частоти .

Інколи спектральну характеристику описують кривими, що являють собою дійсну та уявну частину спектральної функції.

(3.1)

(3.2)

Ці дві криві містять повну інформацію про амплітуду і фазу спектральної характеристики причому - непарна функція, - парна функція, а відтак, якщо функція - парна, то спектр зводиться тільки до дійсної частини , що збігається з . Аналогічно у разі непарної функції спектр зводиться до уявної частини .

Зауваження 1. Спектральну характеристику можна вважати обвідною коефіцієнтів ряду Фур'є, тобто границею лінійчатого спектра частот періодичної функції, коли період функції прагне до нескінченності.

4. Розрахункова частина

У розрахунковій частині даної роботи досліджується неперіодична функція

,

Потрібно знайти:

розклад в інтеграл Фур'є

амплітудний і фазовий спектр.

Розв'язання

а) Функція задовольняє таким умовам теореми Фур’є [4], [5]:

Рис.4.1 Графік досліджуємої неперіодичної функції f (t)

(прямокутний імпульс тривалості t) задана на всій осі . на будь-якому кінцевому відрізку цієї осі задовольняє умовам Дирихле [], а отже розкладається в ряд Фур'є.

Абсолютно інтегрувальна по всій осі, тобто те функція допускає подання у формі інтеграла Фур'є