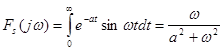Курсовая работа: Перетворення Фур’є. Спектри неперіодичних функцій

Приклад. Побудувати розклад (2.17) для функції

,

Розв‘язок

Тут . Проінтегруємо по проміжку , відповідно (2.2) при отримаємо

Оскільки

, тоді

.

Розклад (2.18), де запишеться як:

2.3 Інтегральне перетворення Фур’є

При дотриманні певних умов у ряд Фур'є розкладається періодична функція, задана на всій дійсній осі, або функція, визначена на кінцевому інтервалі. Розкладання в ряд Фур'є неперіодичної функції, заданої на необмеженому інтервалі, нездійсненно. Однак ідея подання функції нескінченним набором гармонік у декілька зміненій формі реалізована і в цьому випадку. Засобом досягнення мети служить інтеграл Фур'є [3], [4], [5].

Припустимо, що комплексна формула інтеграла Фур'є має місце для всіх значень за винятком скінченої кількості точок.

Тоді

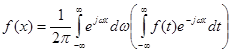(2.18)

Вираз у дужках - функція від . Позначимо цю функцію :

(2.19) тоді

(2.20)

Вирази (2.19) та (2.20) називаються двобічним прямим та оберненим перетворенням Фур'є. Якщо функція при , то дістанемо однобічні перетворення Фур'є.

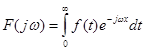(2.21)

(2.22)

Аналогічно, звернувшись до формул (2.9) і (2.10), можна ввести пряме і обернене косинус-перетворення Фур'є для парної функції .

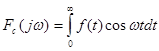(2.23)

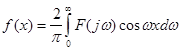(2.24)

та пряме і обернене синус-перетворення Фур'є для непарної функції :

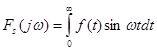(2.25)

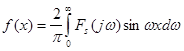(2.26)

Приклад. Знайти прямі косинус - перетворення Фур'є та синус-перетворення функції .

,
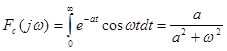