Курсовая работа: Постановка и решение транспортной параметрической задачи

где X_ij – объем поставок груза,

при ограничениях:

Xij≥0,

Пользуясь методом потенциалов, (Фогеля) решаем задачу при k=δ до получения оптимального решения. Признаком оптимальности является условие:

для незанятых клеток

и для занятых клеток,

где – потенциалы строк, столбцов распределительной таблицы.

Условие совместимости транспортной задачи запишется в виде

Значения aij и Bij определяются из условия

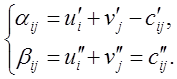
где определяются из систем уравнений

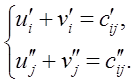
Значения k находятся в пределах k₁ ≤k≤k₂ :

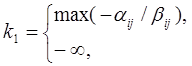
если существует хотя бы одно B_ij >0;

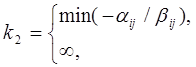
если все B_ij ≥0

если существует хотя бы одно B_ij >0;

если все B_ij ≤0.

Алгоритм решения.

1) Задачу решаем при конкретном значении параметра k=δ до получения оптимального решения.

2) Определяем a_ij и B_ij .

3) Вычисляем значение параметра k.

4) Если k>δ, производим перераспределение поставок и получаем новое оптимальное решение. Если k = δ, то процесс решения окончен [1].

3 Метод решения задачи об оптимальных перевозках средствами Ms Excel

Нахождение оптимального плана перевозок с применением компьютерной программы MsExcelосуществляется посредством функции "Поиск решения".

Схема выполнения: