Курсовая работа: Постановка и решение транспортной параметрической задачи
Табл. 4.3.2 Проверка второго опорного решения на оптимальность методом потенциалов
| заполненные | незаполненные | ||||
| № | vi + uj = cij | значения | № | vi + uj ≤ cij | условие |
| А1 В1 | v1 +u1 =2 | v1 =0, u1 =2 | А1 В3 | v3 +u1 <=2 | соблюдается |
| А1 В2 | v2 +u1 =4 | v2 =2 | А2 В1 | v1 +u2 <=5 | соблюдается |
| A2 B2 | v2 +u2 =5 | u2 =3 | А2 В3 | v3 +u2 <=6 | соблюдается |
| A3 B1 | v1 +u3 =4 | u3 =4 | А3 В2 | v2 +u3 <=7 | соблюдается |
| A3 B3 | v3 +u3 =3 | v3 = -1 | A4 B2 | v2 +u4 <=8 | соблюдается |
| A4 B1 | v1 +u4 =6 | u4 =6 | A4 B3 | v3 +u4 <=1+k | соблюдается |
Решение, полученное при k=4, является оптимальным для всех значений параметра k, удовлетворяющих условию ![]() .
.
Из условия для свободных клеток найдем:
∆13 = a3 + b1 - C'13 = -1 + 2 - 2 = -1
∆21 = a1 + b2 - C'21 = 0 + 3 - 5 = -2
∆23 = a3 + b2 - C'23 = -1 + 3 - 6 = -4
∆32 = a2 + b3 - C'32 = 2 + 4 - 7 = -1
∆42 = a2 + b4 - C'42 = 2 + 6 - 8 = 0
∆43 = a3 + b4 - (C'43 + С''43 ) = -1 + 6 - (1+k) = 4-k
Определение значений k1 и k2
k1 = max(-aij /Bij ) = -a43 /B43 = 4. Все Bij < 0
k2 = min(-aij /Bij ) = ![]() т.к. все Bij ≤ 0
т.к. все Bij ≤ 0
Так как по условию задачи k ≤ 9, то оптимальное решение сохраняется при 4≥k≥9.
При этом минимальная стоимость транспортных расходов составит:
F(X2 )min = 20*6 + 60*3 + 10*4 + 90*2 + 10*4 + 70*5 = 910
Таким образом, при ![]() F(X2 )min = 910 и
F(X2 )min = 910 и
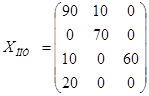 .
.
4.4 Решение задачи средствами Ms Excel
Создадим в окне программы MsExcel две матрицы «План перевозок» и «Стоимость перевозок», согласно вышеизложенным правилам (рис 4.4.1). Также нужно указать ячейку содержащую изменяемый параметр k. При этом в клетке A4 B3 матрицы «Стоимость перевозок» устанавливаем формулу, отображающую зависимость данного тарифа от параметра k: L7=1+L9.
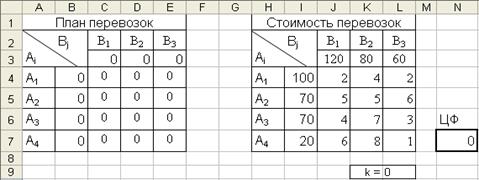
Рис. 4.4.1. Фрагмент окна программы MsExcel: Матрицы «План перевозок» и «Стоимость перевозок» с изменяемым тарифом C43 .
В ячейки, которые должны отображать запасы поставщиков и потребности потребителей в матрице «План перевозок» вводим формулы суммирующие значения всех возможных поставок данных поставщиков и потребителей, например: B4=СУММ(C4:E4), C3=СУММ(С4:С7).
В ячейку целевой функции (N7) введем =СУММПРОИЗВ(C4:E7;J4:L7).
Метод решения параметрической транспортной задачи средствами Ms Excel заключается в нахождении оптимального решения при каждом значении параметра k, с сохранением сценария для каждой процедуры «Поиск решения». После этого необходимо из всего диапазона изменения параметра k выделить отдельные промежутки, на которых сохраняется оптимальное решение задачи и минимальная стоимость затрат.
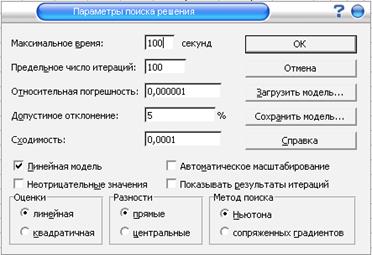
В диалоговом окне «Поиск решения», согласно вышеуказанным правилам установим все необходимые ограничения и ссылки на необходимые ячейки (рис. 4.4.2). Также необходимо в ограничениях указать пределы изменения параметра k, т.е. 0≤k≤9.
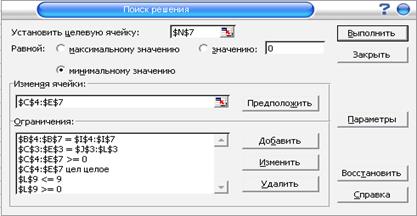
Рис. 4.4.2. Диалоговое окно «Поиск решения»
В диалоговом окне «Параметры поиска решения» установить необходимые параметры (рис. 4.4.3).