Курсовая работа: Постановка и решение транспортной параметрической задачи
После нажатия на кнопку «Выполнить» в диалоговом окне «Результаты поиска решения» (рис. 4.4.5) нажать «Сохранить сценарий…» и в появившемся диалоговом окне «Сохранение сценария» задать имя данному сценарию и нажать «ОК» (рис. 4.4.4.).
Рис. 4.4.4. Диалоговое окно «Сохранение сценария»
После сохранения сценария в диалоговом окне «Результаты поиска решения» выделить необходимые типы отчетов и нажать «OK» (рис. 4.4.5.).
Рис. 4.4.5. Диалоговое окно «Результаты поиска решений
После выполнения всех операций в матрице «План перевозок» получим оптимальный план перевозок при k=0 (рис. 4.4.6.).
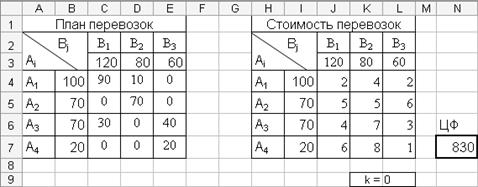
Рис. 4.4.6. Фрагмент окна программы MsExcel: Результат поиска решения при k=0.
Полученное значение целевой функции F(x1 )min =830.
Теперь аналогичным способом найдем оптимальный план перевозок при k=1. Проведя повторный расчет, получим новый план перевозок и значение целевой функции (рис 4.4.7.).
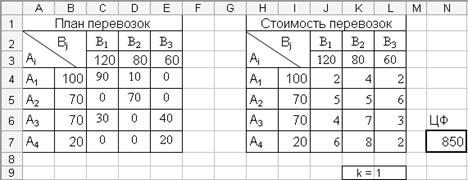
Рис. 4.4.7. Фрагмент окна программы MsExcel: Результат поиска решения при k=1
Полученное значение целевой функции F(x2 )min = 850.
Как видно из рисунков 4.4.5. и 4.4.6 планы перевозок в обоих случаях (k=0, k=1) одинаковы. После дальнейших расчетов при всех остальных значениях параметра kобнаружим, что при 
план перевозок остается неизменным, изменяется лишь значение целевой функции. При значении параметра 
«Поиск решения» выдает другой план перевозок, и значение целевой функции на данном промежутке остается неизменным F(x)min = 910. Полученный план перевозок при значении k=4 изображен на рисунке 4.4.8.
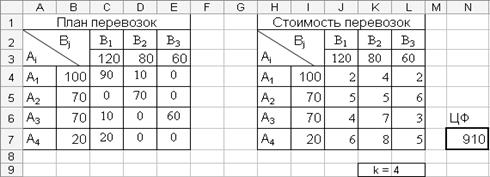
Рис. 4.4.8. Фрагмент окна программы MsExcel: Результат поиска решения при k=4
Значения целевой функции, соответствующие параметру k в каждой итерации представлены в таблице 4.4.1.
Из представленных в таблице 4.4.1 данных можно вывести определенную закономерность изменения значения целевой функции на промежутке :
F(x1 )min = 830, (k=0);
F(x2 )min = F(x1 )min +20 = 830+20, (k=1);
F(x3 )min = F(x2 )min +20 = 830 + 20*2 = 870, (k=2).
Следуя по той же цепочке, найдем:
F(x4 )min = 830 + 20*3, (k=3).
F(x5 )min = 830 + 20*4, (k=4).
Исходя из подобной логики можно представить F(x1 )min = 830 + 20*0.
Отсюда можно вывести формулу, отображающую закономерность изменения значения целевой функции при :
.
Для значений значение функции постоянно F(x)=910.